październik 2015

październik 2015

Data ostatniej modyfikacji:
2015-11-16

Zad. 1. Jaka jest największa możliwa wartość największego wspólnego dzielnika trzech różnych liczb całkowitych dodatnich, których suma wynosi 2015?

Zad. 2. Czy dowolny trójkąt można podzielić na trójkąty równoramienne?

Zad. 3. Jacek i Wacek grają w statki na planszy 9×9. Jacek ukrył na niej lotniskowiec o wymiarach 1×5 lub 5×1. Ile co najmniej strzałów musi oddać Wacek, aby trafić w lotniskowiec?

Wyniki:

W tym miesiącu punkty zdobyli:

3 - Jakub Dobrzański G 3 Lubin, Marek Komorowski G 3 Żory, Wiktor Koropczuk G 3 Gorzów Wielkopolski, Oliwia Kropidłowska G 1 Wrocław, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Krzysztof Mach G 52 Kraków, Karolina Mielczarek G Lewin Brzeski, Iwo Pilecki-Silva G 26 Wrocław, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński, Franciszek Stepek Społeczne G Żary, Ewelina Szymańska G w ZSG Stara Błotnica i Damian Szymański G w ZSG Stara Błotnica;
2 - Aleksandra Domagała G 23 Wrocław, Michał Fabijanowski Niepubliczne G Nasza Szkoła Warszawa, Kacper Gembara G w ZSS Wołów, Przemysław Lewandowski G Sochocin, Julia Mazur G Lewin Brzeski, Bartosz Moszczyński G Lewin Brzeski, Franciszek Sowul G 58 Poznań i Laura Stefanowska G im. św. Franciszka z Asyżu Legnica;
1 - Aleksandra Gołębiowska G 10 Kalisz, Magdalena Gołębiowska G 10 Kalisz, Dawid Konieczko Społeczne G Szprotawa i Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie;
0,5 - Kajetan Walawski G Miejskie Leżajsk.

Pozostali uczestnicy otrzymali poniżej 0,5 punktu.

Odpowiedzi:

Zad. 1. Największy możliwy największy wspólny dzielnik to 155. Rozkład liczby 2015 na czynniki pierwsze to 5·13·31. Niech 2015 = a+b+c = d·(e+f+g). Liczby w ostatnim nawiasie są różne (dlaczego?), więc ich suma wynosi co najmniej 1+2+3 = 6, a uwzględniając rozkład liczby 2015 - co najmniej 13. Stąd d jest równe co najwyżej 5·31 = 155. Wartość ta jest osiągana dla e+f+g = 13, np. 1+5+7, wówczas a+b+c = 155+775+1085 = 2015.

Zad. 2. Trójkąt nieprostokątny dzielimy na dwa prostokątne odpowiednią wysokością. Każdy trójkąt prostokątny można podzielić na dwa równoramienne, łącząc środek przeciwprostokątnej z wierzchołkiem kąta prostego (równoramienność wynika z możliwości wpisania tego trójkąta w okrąg, którego średnicą jest przeciwprostokątna).

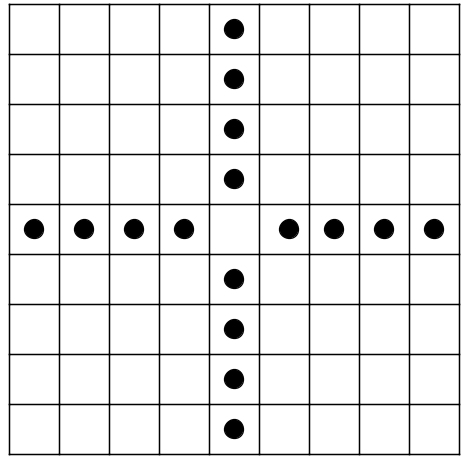
Zad. 3. Podział planszy na 16 rozłącznych prostokątów 1×5 i 5×1 dowodzi, że trzeba strzelić co najmniej 16 razy (jak dokonać takiego podziału planszy?). I tyle razy wystarczy. Przykładowy sposób strzelania pokazuje poniższy rysunek.

Rysunek do zadania 3.