Zad. 1. Znajdź wszystkie liczby pierwsze p, takie że p+2 i p+4 są także liczbami pierwszymi.
Zad. 2. Ile wynosi x4+y4+z4, jeśli x+y+z=0 i x2+y2+z2=m.
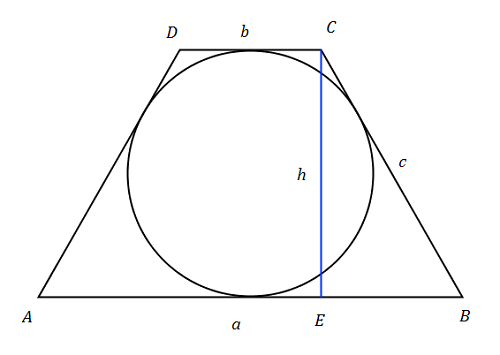
Zad. 3. Udowodnij, że w trapezie równoramiennym opisanym na okręgu wysokość jest średnią geometryczną długości obu podstaw.
W tym miesiącu punkty zdobyli:
- 3 - Jakub Dobrzański G 3 Lubin, Aleksandra Domagała G 23 Wrocław, Michał Fabijanowski
Niep. G Nasza Szkoła Warszawa, Kacper Gembara G w ZSS Wołów, Emilia Kapłon G Żary, Marek Komorowski G 3 Żory, Wiktor Koropczuk G 3 Gorzów Wielkopolski, Oliwia Kropidłowska G 1 Wrocław, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Julia Mazur G Lewin Brzeski, Karolina Mielczarek G Lewin Brzeski, Przemysław Rybarczyk G Integr.Stargard
Szczeciński, Laura Stefanowska G im. św. Franciszka z Asyżu Legnica i Franciszek Stepek Społ. G Żary; - 2,5 - Ewelina Szymańska G w ZSG Stara Błotnica;
- 2 - Bartosz Moszczyński G Lewin Brzeski i Kajetan Walawski G Leżajsk;
- 1,5 - Ewelina Książek ZSS Henryków, Przemysław Lewandowski G Sochocin i Damian Szymański G w ZSG Stara Błotnica;
- 1 - Katarzyna Siomka G Lewin Brzeski;
- 0,5 - Helena John G Wielowieś Świniowice i NN.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po dwóch miesiącach Ligi Zadaniowej z wynikiem 6 pkt. (na 6 możliwych) prowadzą: Jakub Dobrzański, Marek Komorowski, Wiktor Koropczuk, Oliwia Kropidłowska, Joanna Lisiowska, Konrad Litwiński, Karolina Mielczarek, Przemysław Rybarczyk i Franciszek Stepek, drugie miejsce z wynikiem 5,5 pkt. zajmuje Ewelina Szymańska, a trzecie miejsce z wynikiem 5 pkt. zajmują: Aleksandra Domagała, Michał Fabijanowski, Kacper Gembara, Julia Mazur i Laura Stefanowska. Gratulujemy!
Zad. 1. Liczba 3 jest jedyną spełniającą warunki zadania. Liczba pierwsza większa od 3 nie dzieli się przez 3, wiec daje z dzielenia przez 3 resztę 1 lub 2. Niech p będzie postaci 3n+1, dla n = 0, 1, ... Wtedy p+2 = 3n+3 jest liczbą złożoną, bo dzieli się przez 3. Natomiast gdy p jest postaci 3n+2, to p+4 = 3n+6 jest liczbą złożoną. Zatem 3 jest jedynym rozwiązaniem zadania.
Zad. 2. Podnosząc do kwadratu obie strony równania x+y+z = 0,
dostajemy x2+y2+z2+2(xy+xz+yz) = 0,
czyli xy+xz+yz = -m/2.
Podnosząc obustronnie do kwadratu ostatnią równość,
dostajemy x2y2+x2z2+y2z2+2xyz(x+y+z) = 1/4 m2.
Stąd x2y2+x2z2+y2z2 = 1/4 m2.
Podnosząc zaś obustronnie do kwadratu równość x2+y2+z2 = m,
dostajemy x4+y4+z4+2(x2y2+x2z2+y2z2) = m2,
czyli x4+y4+z4 = 1/2 m2.
Zad. 3. Ponieważ trapez jest opisany na okręgu, mamy a+b = 2c, skąd c = a+b/2. Z twierdzenia Pitagorasa dla trójkąta BCE dostajemy h2 = 1/4 (a+b)2 – 1/4 (a–b)2 = ab. Stąd h=√ab.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
