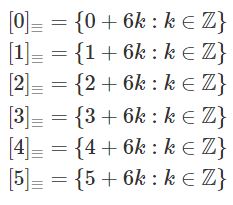Z geometrii znacie figury przystające. Okazuje się, że pojęcie przystawania funkcjonuje też w arytmetyce, gdzie przystawać mogą liczby (i wcale nie muszą być równe). Gdy rozwiązujemy zadania, zwykle interesuje nas to, czy jakieś liczby są równe, jednak to podejście nie zawsze jest optymalne. W równaniu 2x = 4x–1 lewa strona jest zawsze parzysta, a prawa - nieparzysta (nigdy nie są przystające ze względu na podzielność przez 2), zatem pierwiastków całkowitych być nie może.
Kongruencje, czyli czasami lepiej wiedzieć mniej
Gdy funkcja jest niewiadomą - równania funkcyjne
Równań, w których szukamy liczb spełniających jakiś warunek, nikomu nie trzeba specjalnie przedstawiać. Znacie je dobrze ze szkoły. Teraz zajmiemy się równaniami, w których szukamy wszystkich funkcji spełniających pewien warunek. Równania funkcyjne (bo tak je nazywamy) są trudniejsze od równań szkolnych, bo nie ma algorytmu na ich rozwiązywanie - każde jest inne. Są jednak pewne metody, które dają się dość często stosować. Poznajmy je.
Z okręgiem Eulera w tle
Okrąg Eulera zwany też okręgiem Feuerbacha albo okręgiem dziewięciu punktów jest to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Okrąg ten zrobił niebywałą karierę w geometrii i stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności. Poniżej uzasadnimy kilka z nich. C.d.n.
Minimaksy w geometrii elementarnej
Zadania optymalizacyjne, czyli polegające na znajdowanie minimum lub maksimum pewnych zmieniających się wielkości, kojarzą się większości licealistów z użyciem pochodnych. Ale wiele takich zadań można znaleźć także w dziedzinie geometrii elementarnej. Do ich rozwiązania nie są oczywiście potrzebne metody rachunku różniczkowego.
5 komentarzy
Czytaj dalej
Wokół okręgu Eulera
Okrąg Eulera zwany powszechnie okręgiem dziewięciu punktów to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Okrąg ten zrobił niebywałą karierę w geometrii i stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności. O niektórych pisaliśmy już w artykule Z okręgiem Eulera w tle. Teraz poznamy kolejne.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
