Zad. 1. Udowodnij, że dla każdej liczby naturalnej n liczba 2n3+n jest podzielna przez 3.
Zad. 2. Dwa pola pszenicy, jedno czterokrotnie większe od drugiego, są koszone przez pewną liczbę kombajnów zbożowych. Większe pole wszystkie kombajny koszą półtora dnia, następnie połowa z nich zaczyna kosić mniejsze pole, a pozostała połowa kombajnów nadal kosi duże pole. Na koniec drugiego dnia większe pole jest skoszone, a mniejsze musi być koszone jeszcze przez 3 kombajny przez jeden dzień. Ile kombajnów brało udział w koszeniu pierwszego dnia?
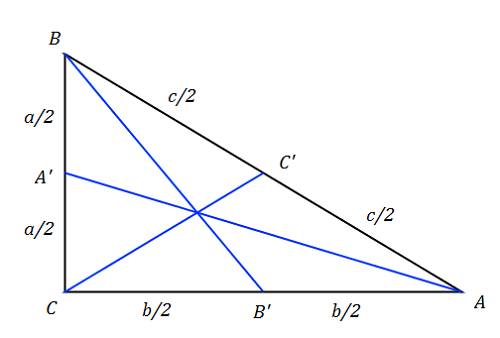
Zad. 3. Oblicz długości środkowych trójkąta prostokątnego o przyprostokątnych a i b.
W tym miesiącu punkty zdobyli:
- 3 - Jakub Dobrzański G 3 Lubin, Aleksandra Domagała G 23 Wrocław, Kacper Gembara G w ZSS Wołów, Wiktor Koropczuk G 3 Gorzów Wielkopolski, Oliwia Kropidłowska G 1 Wrocław, Ewelina Książek ZSS Henryków, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Julia Mazur G Lewin Brzeski, Przemysław Rybarczyk G Integr. Stargard, Katarzyna Siomka G Lewin Brzeski, Laura Stefanowska G im. św. Franciszka z Asyżu Legnica i Kajetan Walawski G Leżajsk;
- 2,5 - Marek Komorowski G 3 Żory i Franciszek Stepek Społ. G Żary;
- 2 - Emilia Kapłon G Żary, Krzysztof Mach G 52 Kraków i Karolina Mielczarek G Lewin Brzeski;
- 1 - Helena John G Wielowieś Świniowice;
- 0,5 - Michał Fabijanowski Niep. G Nasza Szkoła Warszawa i NN.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po trzech miesiącach Ligi Zadaniowej z wynikiem 9 pkt. (na 9 możliwych) prowadzą: Jakub Dobrzański, Wiktor Koropczuk, Oliwia Kropidłowska, Joanna Lisiowska, Konrad Litwiński i Przemysław Rybarczyk, drugie miejsce z wynikiem 8,5 pkt. zajmują: Marek Komorowski i Franciszek Stepek, a trzecie miejsce z wynikiem 8 pkt. zajmują: Aleksandra Domagała, Kacper Gembara, Julia Mazur, Karolina Mielczarek i Laura Stefanowska. Gratulujemy!
Zad. 1. Dla n=1 jest to liczba 3 i jest podzielna przez 3. Dla n>1 liczbę 2n3+n możemy zapisać jako 2n(n−1)(n+1) + 3n. Drugi składnik tej sumy jest podzielny przez 3, natomiast pierwszy składnik jest podwojonym iloczynem trzech kolejnych liczb naturalnych; jedna z nich musi być wielokrotnością trójki, więc ten składnik też jest podzielny przez 3. To oznacza, że liczba 2n3+n jest podzielna przez 3 dla każdej liczby naturalnej n.
Zad. 2. Niech x oznacza liczbę wszystkich kombajnów. Całkowity czas koszenia pola przez pojedynczy kombajn jest proporcjonalny do powierzchni, więc dla dużego pola będzie 4 razy dłuższy.
Zachodzi zatem zależność x·1,5 + x/2·1/2 = 4(x/2·1/2 + 3·1). Stąd x = 16.
Zad. 3. Długość środkowej CC' poprowadzonej z wierzchołka kąta prostego jest równa połowie długości przeciwprostokątnej trójkąta, co wynika z twierdzenia odwrotnego do twierdzenia o kącie wpisanym opartym na średnicy okręgu. Zatem długość tej środkowej z twierdzenia Pitagorasa wynosi [tex]\frac{c}{2}= \frac{1}{2}\sqrt{a^2+b^2}[/tex].
Środkowe AA' i BB' są przeciwprostokątnymi trójkątów prostokątnych o przyprostokątnych a/2 i b oraz a i b/2, zatem ich długości wynoszą z twierdzenia Pitagorasa odpowiednio
|AA'| = [tex]\sqrt{\frac{1}{4}a^2+b^2}[/tex] i |BB'| = [tex]\sqrt{a^2+\frac{1}{4}b^2}[/tex] .
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
