luty 2022

luty 2022

Data ostatniej modyfikacji:
2022-07-13

Zad. 1. W zapisie: [tex] \sqrt[*]{**}=* [/tex] gwiazdki zastępują różne cyfry parzyste. Jakie to działanie?

Zad. 2. Czy istnieje trójkąt o bokach długości 2021²⁰²¹, 2022²⁰²², 2023²⁰²³? Odpowiedź uzasadnij.

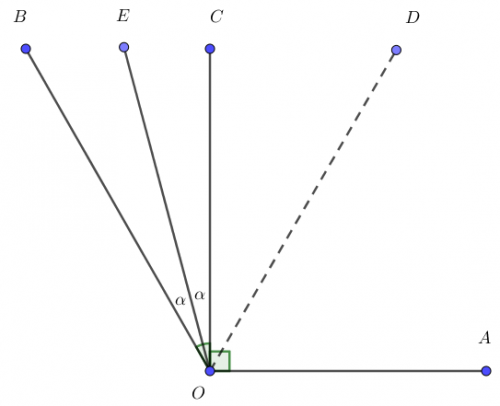
Zad. 3. Wewnątrz kąta rozwartego AOB poprowadzono trzy półproste OC, OD, OE, przy czym OC jest prostopadła do OA, OD jest dwusieczną kąta AOB, a OE jest dwusieczną kąta BOC. Oblicz miarę kąta DOE.

Wyniki:

W lutym punkty zdobyli:

3 – Faustyna Doliwka SP Łobżenica, Dominika Miturska SP 66 Warszawa, Joanna Nowakowska SP 3 Głogów, Igor Sudyka SP 2 Jasło, Miłosz Zakrzewski SP Gostycyn, Amelia Żuczek SP 2 Wieliczka;
2,5 – Artur Bumażnik SP 1 Piechowice, Klara Kogut SP 9 Gliwice, Aniela Przystał SP Ciechów, Alicja Szwarczyńska SP Kowalowa;
2,25 - Dominika Wojdacz SP 11 Inowrocław;
2 – Monika Budzeń SP 7 Leszno, Mateusz Galik SP Arka, Aleksander Kiszkowiak SP 66 Warszawa, Mateusz Koba SP 3 Cieszyn, Michał Licznarowski SP 66 Warszawa, Paweł Lisztwan SP 3 Mikołów, Wiktoria Pietrzak SP 3 Głogów, Arkadiusz Piwowarczyk SP 14 Ostrowiec Świętokrzyski, Bartosz Podlak SP 3 Cieszyn, Oliwia Raszewska SP 6 Boguszów-Gorce, Oliwia Stańczyk SP Aslan, Anastasia Yakovleva SP 3 Mogilno;
1 – Adrian Jasiński SP 42 Wrocław, Marta Pieczonka SP 3 Cieszyn.

Pozostali uczestnicy otrzymali poniżej 1 punktu

Odpowiedzi:

Zad. 1. Dwucyfrowa liczba pod pierwiastkiem jest potęgą parzystą liczby jednocyfrowej parzystej, więc może to być tylko jedna z liczb 4²=16, 6²=36, 8²=64, 2⁴=16, 2⁶=64, bo pozostałe potęgi są już co najmniej trzycyfrowe. Z tych liczb tylko 64=8² spełnia warunki zadania. Ostatecznie [tex] \sqrt[2]{64}=8 [/tex].

Zad. 2. Zauważmy, że 2021²⁰²¹ + 2022²⁰²² < 2^.2022²⁰²²< 2022^.2022^{2022 =}2022²⁰²³<2023²⁰²³. Trójkąt, więc nie istnieje. Nie jest spełniony warunek trójkąta.

Zad. 3. Zauważmy, że |∡DOE| = ¹/₂|∡AOB|–α =¹/₂(90°+2α)–α = 45°+α–α = 45°.