Dwusieczna kąta

Definicja:
Zbiór punktów płaszczyzny/przestrzeni leżących w równej odległości od ramion kąta płaskiego / ścian kąta dwuściennego.

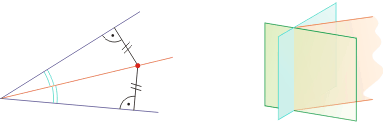
 Własności:

• Dwusieczna kąta płaskiego to prosta (dla kąta dwuściennego - płaszczyzna) przechodząca przez wierzchołek kąta (dla kąta dwuściennego przez krawędź) i dzielącą go na dwa kąty przystające (stąd nazwa: dwu-sieczna = krojąca na połowy).
• Dwusieczna jest jedyną osią symetrii kąta.
• W każdym kącie płaskim dwusieczną można skonstruować cyrklem i linijką.

rysunek

• Dwusieczne kątów trójkąta przecinają się w jednym punkcie (w środku okręgu wpisanego w trójkąt).

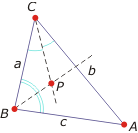
Dowód. Dwusieczne dwóch kątów trójkąta nie są równoległe, więc przecinają się. Oznaczmy punkt ich przecięcia przez P. P leży na dwusiecznej kąta C, więc w równych odległościach od boków a i b. P leży też na dwusiecznej kąta B, zatem w równych odległościach od boków a i c. Skoro P leży w tej samej odległości od boków b i c, to leży na dwusiecznej kąta A, jest więc punktem wspólnym trzech dwusiecznych.

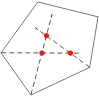
• Dwusieczne kątów czworokąta wypukłego przecinają się w jednym punkcie wtedy i tylko wtedy, gdy sumy długości przeciwległych boków tego czworokąta są równe.

Dowód twierdzenia prostego widać na rysunku. Dowód twierdzenia odwrotnego robi się nie wprost, wykorzystując twierdzenie proste.

• Dwusieczne kątów pewnego wielokąta przecinają się w jednym punkcie wtedy i tylko wtedy gdy można ten wielokąt opisać na okręgu (można w ten wielokąt wpisać okrąg).

         

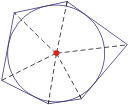
• Twierdzenie o dwusiecznej - dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok proporcjonalnie do długości pozostałych boków.

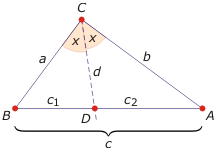
Dowód. Stosunek pól trójkątów o równej wysokości jest równy stosunkowi długości ich podstaw, na które tę wysokość opuszczono. Zatem $\frac{P_{\triangle ADC}}{P_{\triangle BCD}}=\frac{c_2}{c_1} $. Ze wzoru na pole trójkąta lewą stronę można zapisać jako $ \frac{\frac{1}{2} bd\sin x}{\frac{1}{2} ad \sin x}= \frac{b}{a} $. Stąd $\frac{c_2}{c_1}=\frac{b}{a} $.

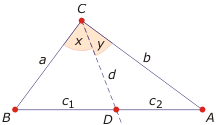
• Uogólnione twierdzenie o dwusiecznej - jeśli punkt D dzieli bok AB trójkąta ABC w stosunku c₁:c₂, a półprosta CD dzieli kąt C w stosunku x:y, to zachodzi: $\frac{c_1}{c_2}= \frac{a \sin x}{b \sin y}$ .

• Twierdzenie o dwusiecznej kąta zewnętrznego - w trójkącie o wierzchołkach A, B, C dwusieczna kąta zewnętrznego tworzy na przedłużeniu przeciwległego boku odcinki proporcjonalne do pozostałych boków, tzn. zachodzi: $\frac {AC}{BC}=\frac {AZ}{BZ}$.

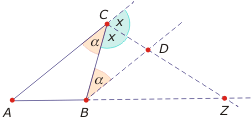
Dowód. Z wierzchołka B prowadzimy prostą równoległą do boku AC, otrzymując w przecięciu z dwusieczną punkt D. Trójkąty ACZ i BDZ są podobne (cecha KKK), stąd mamy: $\frac {AZ}{BZ}=\frac {AC}{BD}$. Trójkąt BCD jest równoramienny (kąty typu Z o mierze α oraz α+x+x = 180º), więc otrzymujemy brakującą do tezy równość BD=BC.

• symetralna
• sieczna
• trójsieczna
• wielokąt cykliczny
• czworokąt cykliczny