Adam Kochański herbu Lubicz [1631-1700] to największy polski matematyk XVII wieku, a ponadto filozof, fizyk, astronom i mechanik precyzyjny. Po wstąpieniu do zakonu przyjął imię Adamandy (z łac. ad amandi, czyli z Kochania, co było zlatynizowaną formą jego nazwiska). Był jezuitą, nadwornym kapelanem, bibliotekarzem, matematykiem, zegarmistrzem i astronomem króla Jana III Sobieskiego i wychowawcą jego synów (zwłaszcza najstarszego - księcia Jakuba). Znany jest głównie ze zmyślnej konstrukcji przybliżonej kwadratury koła. Przez trzy lata mieszkał we Wrocławiu i uczył matematyki w Kolegium Jezuickim, przekształconym później w uniwersytet.
 Kochański urodził się w Dobrzyniu nad Wisłą. Uczył się w szkole średniej w Toruniu, a w 1652 roku wstąpił do zakonu jezuitów w Wilnie i rozpoczął na tamtejszej akademii studia filozoficzne. Szybko dał się poznać, jako doskonały matematyk. W 1655 w obawie przed nadciągającymi wojskami moskiewskimi opuścił miasto i przez wiele lat podróżował po ośrodkach naukowych Europy, początkowo uzupełniając wykształcenie (Würzburg 1656, Molsheim 1657), a potem prowadząc wykłady z matematyki (Moguncja 1658-1664, Florencja 1665-1670, Praga 1671-1672 i Ołomuniec 1673-1675), aż w roku 1676 dotarł do Wrocławia, gdzie wykładał do 1680. Później na zaproszenie króla Jana III Sobieskiego wrócił do Polski.
Kochański urodził się w Dobrzyniu nad Wisłą. Uczył się w szkole średniej w Toruniu, a w 1652 roku wstąpił do zakonu jezuitów w Wilnie i rozpoczął na tamtejszej akademii studia filozoficzne. Szybko dał się poznać, jako doskonały matematyk. W 1655 w obawie przed nadciągającymi wojskami moskiewskimi opuścił miasto i przez wiele lat podróżował po ośrodkach naukowych Europy, początkowo uzupełniając wykształcenie (Würzburg 1656, Molsheim 1657), a potem prowadząc wykłady z matematyki (Moguncja 1658-1664, Florencja 1665-1670, Praga 1671-1672 i Ołomuniec 1673-1675), aż w roku 1676 dotarł do Wrocławia, gdzie wykładał do 1680. Później na zaproszenie króla Jana III Sobieskiego wrócił do Polski.
W czasie pobytu we Wrocławiu Kochański nie tylko uczył matematyki w Kolegium Jezuickim, ale zajmował się także astronomią. To właśnie będąc w naszym mieście, nawiązał wieloletnią korespondencję współpracę z Janem Heweliuszem z Gdańska, która zaowocowała m. in. wspólną konstrukcją słynnego stiukowego zegara słonecznego w rezydencji królewskiej w Wilanowie (1680) uważanego do dziś za najwspanialszy zegar słoneczny w Europie. Po śmierci Heweliusza w 1686 roku Kochański jeździł do Gdańska w celu pozyskania do zbiorów królewskich spuścizny po zmarłym astronomie.
Poniżej prezentujemy zdjęcie zegara z Wilanowa. Na głównej tarczy wskazówkę (pióro) trzyma bóg czasu Chronos, w drugiej ręce trzyma kosę - symbol przemijania. Na bocznych polach umieszczone są podziałki z godzinami babilońskimi (wskazuje czas, jaki minął od wschodu słońca) i włoskimi (czas, jaki pozostał do zachodu słońca). Draperia, na której rozmieszczono tarcze podtrzymywana jest przez putta. Wokół głównej tarczy umieszczone są znaki zodiaku (symbolizujące miesiące) i symbole dni tygodnia, znaki przedstawiające tematykę zainteresowań jego twórców: księżyc, planety, lustro i magnes. Złote dzwonki rozmieszczone na tarczy wskazują momenty dzwonienia rannego, południowego i wieczornego (sygnały oznaczające rozpoczęcie dnia pracy, przerwę obiadową i jego zakończenie).

Wśród pism Kochańskiego znajduje się także rozprawa na temat heliocentryzmu i poglądów Mikołaja Kopernika oraz bogata korespondencja z Gotfrydem Leibnizem, która wskazuje, że jako pierwszy z Polaków poznał teorię rachunku różniczkowego i to z pierwszej ręki (listy te ogłosił drukiem polski matematyk Samuel Dickstein w latach 1901-1902).
Jako mechanik Kochański był znanym teoretykiem i konstruktorem zegarów. Jego dzieło "Mirabilia Chronometrica" (cuda pomiaru czasu) ogłoszone w 12-tomowym dziele znanego matematyka Gaspara Schotta "Technica Curiosa" w Würzburgu w 1664 roku uważane jest w literaturze europejskiej za najstarszy podręcznik zegarmistrzostwa obejmujący zegary mechaniczne. Kochański zajmował się problemem dokładnego pomiaru czasu umożliwiającego pomiar długości geograficznej na morzu. Od czasów Galileusza i opisu ruchu wahadła, problem ten zajmował największych matematyków w Europie. W 1656 pierwszy dokładny zegar z wahadłem tautochronicznym skonstruował holenderski matematyk Christian Huygens (jego praca Horologium oscillatorium ma w historii nauki miejsce równe pracom Kopernika, Galileusza i Newtona). Natomiast Kochański już w 1659 roku zaproponował zastąpienie wahadła balansem kołowym z napędem sprężynowym, a w 1667 zbudował też zegarek kieszonkowy z wahadłem magnetycznym. Zaproponował też ustandaryzowanie liczby wahnięć wahadła na godzinę (7200 lub 10800 to jest 2-3 na sekundę) - wcześniej każdy zegarmistrz regulował to dowolnie. Zajmował się też konstrukcją maszyny liczącej i kwadratami magicznymi.
 W 1682 roku w Lipsku grono uczonych założyło najważniejsze ówczesne czasopismo naukowe "Acta Eruditorum", w którym w 1684 ukazała się praca Leibniza dająca podstaw rachunku różniczkowego. Rok później w piśmie tym ukazała się rozprawa Kochańskiego o przybliżonej rektyfikacji (wyprostowaniu) okręgu, czyli o konstrukcji odcinka o długości bliskiej obwodowi danego okręgu. Do dziś uznana jest ona za jedną z najprostszych i najpiękniejszych, m.in. dlatego, że niezmienna pozostaje w niej początkowa rozwartość cyrkla. Rysunek obok przedstawia tę konstrukcję, z ponumerowanymi kolejnymi krokami (z punktu 6 promień odkładany jest trzy razy). Długość odcinka pomiędzy punktami 3 i 9 wyliczona z twierdzenia Pitagorasa przybliża długość półokręgu i daje wartość liczby π z błędem rzędu 0,002%.
W 1682 roku w Lipsku grono uczonych założyło najważniejsze ówczesne czasopismo naukowe "Acta Eruditorum", w którym w 1684 ukazała się praca Leibniza dająca podstaw rachunku różniczkowego. Rok później w piśmie tym ukazała się rozprawa Kochańskiego o przybliżonej rektyfikacji (wyprostowaniu) okręgu, czyli o konstrukcji odcinka o długości bliskiej obwodowi danego okręgu. Do dziś uznana jest ona za jedną z najprostszych i najpiękniejszych, m.in. dlatego, że niezmienna pozostaje w niej początkowa rozwartość cyrkla. Rysunek obok przedstawia tę konstrukcję, z ponumerowanymi kolejnymi krokami (z punktu 6 promień odkładany jest trzy razy). Długość odcinka pomiędzy punktami 3 i 9 wyliczona z twierdzenia Pitagorasa przybliża długość półokręgu i daje wartość liczby π z błędem rzędu 0,002%.
Wykonaj samodzielnie potrzebne obliczenia.
Od 1695 roku Kochański przebywał na leczeniu w czeskich Teplicach, gdzie pracował nad wynalezieniem panaceum i perpetuum mobile. Zajmował się też opracowaniem języka uniwersalnego idioma catholicum, wyprzedzając tym samym o 200 lat esperanto. Ostatni list napisał do Leibniza w czerwcu 1698 r. Potem była już tylko długa i ciężka choroba – postępujący paraliż. Zmarł w 1700 roku i został pochowany w miejscowym kościele przypałacowym.
Literatura:
- http://www.forumakad.pl/archiwum/2007/01/53_matematyk_i_konstruktor_zega...
- http://zegarkiclub.pl/?dir=historia/osoby/03
- http://kochanscy.pl/biogramy-slawnych-osob/
- http://gnomonika.pl/katalog.php?id=4


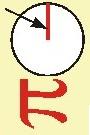





odległość między punktami 3 i 9
Odległość między tymi punktami przybliża połowę obwodu okręgu czyli pi, a więc przy założeniu, że r=1 będzie to liczba 3,141533339