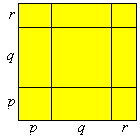
 (p + q + r) 2 =
p2 +
q2 +
r2 +
2pq +
2pr +
2qr.
(p + q + r) 2 =
p2 +
q2 +
r2 +
2pq +
2pr +
2qr.
Ten wzór jest prawdziwy dla wszystkich liczb.
Wystarczy mozolnie pomnożyć (p + q + r)(p + q + r) i już.
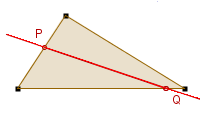 Na rysunku obok prosta PQ dzieli trójkąt na dwie części o równych polach i obwodach.
Na rysunku obok prosta PQ dzieli trójkąt na dwie części o równych polach i obwodach.
Czy dla dowolnego trójkąta istnieje prosta dzieląca go
na dwie części o równych polach i obwodach?
Dla trójkątów osiowosymetrycznych (czyli trójkątów równoramiennych) oś symetrii oczywiście dzieli i pole, i obwód na połowy.
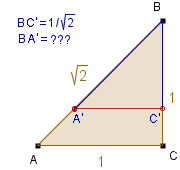
W trójkącie równoramiennym prostokątnym nie tylko oś symetrii dzieli obwód i pole na połowy. Na rysunku obok prosta A'C' || AC, gdzie BC' =
1/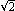 , też jest dobra. Sprawdź!
, też jest dobra. Sprawdź!
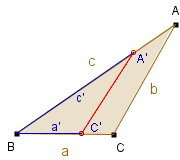
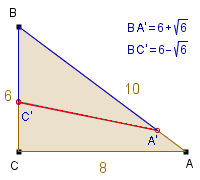 Na rysunku obok prosta A'C' dzieli trójkąt ABC na dwie części o równych obwodach, bowiem wystarczy sprawdzić (dlaczego?), że
Na rysunku obok prosta A'C' dzieli trójkąt ABC na dwie części o równych obwodach, bowiem wystarczy sprawdzić (dlaczego?), że
BA' + BC' =
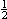 (AB + AC + BC).
(AB + AC + BC).
Porównując podstawy trójkątów, zauważamy, że
P BA'C' =
BC'/BC .
P
BA'C' =
BC'/BC .
P BA'C
= BC'/BC . BA'/BA .
P
BA'C
= BC'/BC . BA'/BA .
P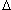 BAC.
BAC.
Zatem prosta A'C' połowi pole, gdy
BA' . BC' =
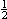 . BA . BC
. BA . BC
Tak jest w istocie, bo
(6-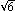 ) .
(6+
) .
(6+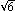 ) =
62 - 6 = 30 =
) =
62 - 6 = 30 =
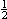 . 10 . 6.
. 10 . 6.
 Twierdzenie 1.
Twierdzenie 1.
W trójkącie ABC niech
a=BC, b=AC, c=AB i
a b
b c.
c.
Niech A', C' leżą na bokach BA, BC i
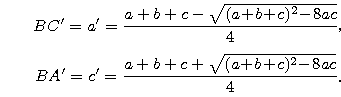
Wtedy prosta A'C' dzieli pole i obwód trójkąta ABC na połowy.
Dowód
* Nietrudno sprawdza się, że prosta A'C' dzieli obwód trójkąta ABC na połowy:
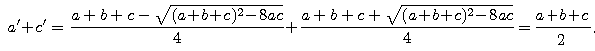
* Prosta A'C' dzieli pole trójkąta ABC na połowy, bo widać, że a'c' = 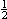 . ac, bowiem
. ac, bowiem
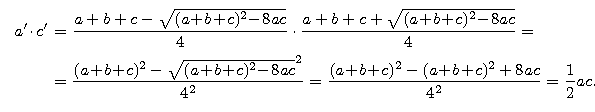
To nie koniec dowodu. Trzeba jeszcze sprawdzić kilka nierówności.
* Wyrażenie pod pierwiastkiem jest nieujemne, bo
* a' 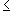 a, bo
a, bo
* c' 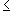 c, bo
c, bo
* 0 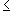 c', bo
c', bo
* 0 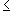 a', bo
a', bo

Uwaga 1
Przy założeniach jak w twierdzeniu 1 można pokazać, że
A'C' || AC wtedy i tylko wtedy, gdy b = (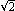 -1)(a+c),
-1)(a+c),
bowiem
Uwaga 2
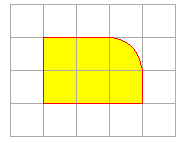
Czy dla figury obok istnieje prosta, która dzieli jej pole i obwód na połowy?
To zadanie jest beznadziejne rachunkowo, tzn. wyznaczenie takiej prostej wzorem jest niemożliwe.
Jednak można łatwo uzasadnić istnienie takiej prostej.
Uwaga 3
W tekstach:
Wszystkie połowiące pole trójkąta,
Wszystkie połowiące obwód trójkąta,
Połowiące trójkąta w zadaniach
badaliśmy oddzielnie obie własności połowienia. Zajrzyj tam koniecznie.

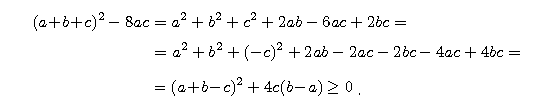
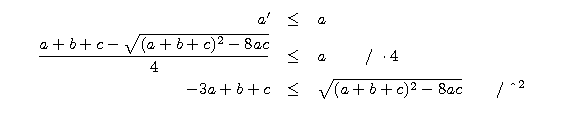
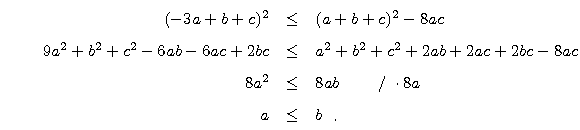
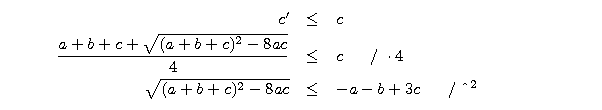
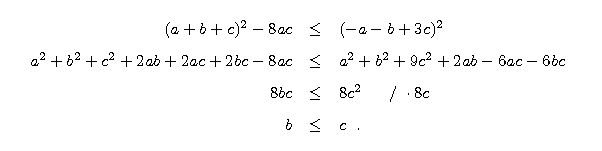
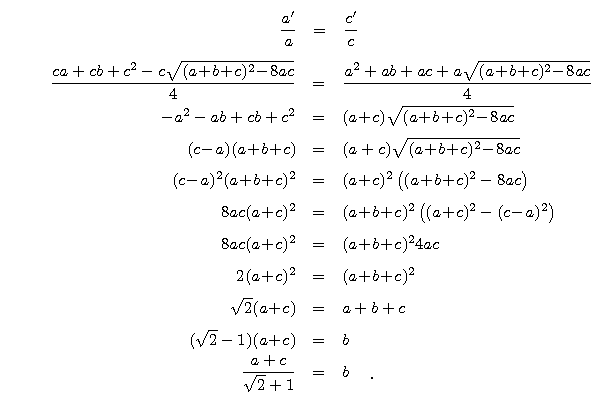


 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.



Zagadki
Nieźle się przy tym nagłowiłem :)
Dzień dobry, skąd
Dzień dobry, skąd właściwie wzięły się równości:
a' = (a+b+c - √(a+b+c)^2 - 8ac)/4
c' = (a+b+c + √(a+b+c)^2 - 8ac)/4