Nieziemskie przyciąganie (przeskalowanie) jest kolejnym przykładem omyłkowego przeksztalcenia (porównaj z Omyłkowe przekształcenia - orsymetria lub Omyłkowe przekształcenia - emsymetria). Poznaj podstawowe własności tego przekształcenia i rozwiąż kilka ciekawych zadań.
Dla figury (domkniętej) wypukłej c, punktu Z i liczby s >0 określamy:
Zc = punkt z c leżący najbliżej Z,
Z' = punkt z półprostej ZcZ taki, że
ZcZ' = s . ZcZ .
Ponadto, dla figury u symbol u' = Pcs ( u )
oznacza figurę utworzoną z punktów Z', dla Z z u.
Można myśleć, że figura c jest magnesem, który przyciąga do siebie lub odpycha od siebie (dla s>1) punkty w zadanej skali s, podobnie jak jednokładność przyciąga lub odpycha punkty do/od magnesu c będącego punktem.
Poniżej widać efekt przekształcenia Pcs dla różnych wielokątów (można zmieniać wierzchołki i położenia całych figur). Kluczem do zrozumienia tego przekształcenia jest zbadanie, co jest obrazem odcinka w tym przekształceniu, w których miejscach obraz odcinka 'załamuje się'.
Rysunek dynamiczny utworzony w GeoGebrze.
Dla s = 1/2 punkt Z' jest środkiem odcinka łączącego Z z najbliższym punktem z c,
a u' = Pc1/2 ( u ) jest zbiorem wszystkich tych środków dla Z z u.
Poniższe zadania są pochodzą z konkursu KoMa 2014.
Trudniejsze zadania to: 4.c, 7.c, 8 i 9.
1. Narysuj
u' = Pc1/2 ( u )
i
v' = Pc1/2 ( v )
(efekt przeskalowania u i v względem c w skali 1/2).
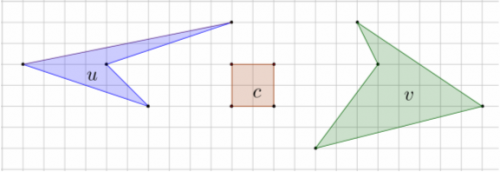
a) Ile boków ma u' ? . . .
b) Ile boków ma v' ? . . .

2. a) u' = Pc1/2 ( u )
Ile boków ma u' ? . . .
pole u' = . . .

2. b) v' = Pc1/2 ( v )
Ile boków ma v' ? . . .
pole v' = . . .

2. c) w' = Pc1/2 ( w )
Ile boków ma w' ? . . .
pole w' = . . .

3. a) u' = Pc1/2 ( u )
Ile boków ma u' ? . . .
pole u' = . . .

3. b) v' = Pc1/2 ( v )
Ile boków ma v' ? . . .
pole v' = . . .

3. c) w' = Pc1/2 ( w )
Ile boków ma w' ? . . .
pole w' = . . .
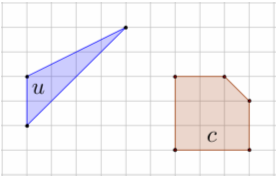
4. a) pole
Pc1/4 ( u ) = . . .
4. b) pole
Pc3/4 ( u ) = . . .
4. c) pole
Pc4/5 ( u ) = . . .
5. Narysuj takie u i v, że
u' = Pc1/2 ( u ),
v' = Pc1/2 ( v )
są przedstawione na rysunku.

a) Ile boków ma u' ? . . .
b) Ile boków ma v' ? . . .
pole u = . . .
pole v = . . .
6. Narysuj takie u i v, że
u' = Pc1/2 ( u ),
v' = Pc1/2 ( v )
są przedstawione na rysunku.
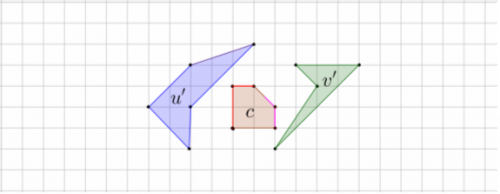
a) Ile boków ma u' ? . . .
b) Ile boków ma v' ? . . .
pole u = . . .
pole v = . . .

7.
Znajdź taką wartość h > 0, że:
a)
Pc1/2 ( u ) ma pole 9
b)
Pc1/2 ( u ) ma pole 12
c)
u ma pole 2 razy większe niż
Pc1/2 ( u )

8.
Znajdź taką wartość s > 0, że:
a)
Pcs ( u ) jest trójkątem
b)
jeden z kątów Pcs ( u ) ma 90o
c)
Pcs ( u ) ma pole 2.
9.
Graniastosłup s ma wierzchołki o współrzędnych:
a) liczba wierzchołków u' = . . . . b) liczba krawędzi u' = . . . . c) liczba ścian u' = . . . .
d) objętość u' = . . . . e) pole powierzchni u' = . . . . e) suma długości krawędzi u' = . . . .
Szerzej o tym przekształceniu piszemy w tekście Nieziemskie przyciąganie, który podsumowuje obserwacje z powyższych zadań.