|
Wszystkie rysunki utworzono za pomocą programu C.a.R. Można przesuwać 'wypełnione' punkty. |
Na lekcji pani podała, jak konstrukcyjnie znaleźć punkt P' będący odbiciem punktu P w prostej m:
- kreślimy z P prostą n prostopadłą do m,
- punkt przecięcia n z m oznaczamy przez Pm,
- kreślimy okrąg o środku Pm przechodzący przez P,
- P' jest punktem przecięcia okręgu z n (różnym od P).
Na rysunku można obejrzeć tę konstrukcję dla punktów P, Q i T.
Karol, jak to Karol, niby słuchał uważnie, jednak omyłkowo przyjął, że
Na rysunku można obejrzeć tę konstrukcję dla punktów P, Q i T.
Sprawdź, że wszystko się zgadza! Mamy bowiem:
- prosta n przechodzi przez P i jest prostopadła do m,
- punkt przecięcia n z m oznaczony jest przez Pm,
- wykreślony jest okrąg o środku Pm przechodzący przez P,
- P' jest punktem przecięcia okręgu z n (różnym od P).
Nazwijmy to przekształcenie orsymetrią (albo OR-symetrią).
Zbadamy, jakie ma ono własności.
Powyższy przepis szwankuje dla punktu O będącego środkiem okręgu m. Wtedy każda prosta przechodząca przez O jest prostopadła do okręgu i nie można wyznaczyć punktu O'. Co zrobić z tym fantem?
To samo, co robimy w przypadku funkcji y = 1/x. Tu przepis szwankuje dla x = 0, więc przyjmujemy, że liczba 0 nie należy do dziedziny funkcji. Podobnie przyjmiemy, że punkt O nie należy do dziedziny OR-symetrii.
Proste własności OR-symetrii zebrane są w poniższym zadaniu.
Przyjmujemy standardowe oznaczenia, w szczególności:
- o(A, r) oznacza okrąg o środku A i promieniu r,
- k(A, r) oznacza koło o środku A i promieniu r,
- P' oznacza obraz punktu P w OR-symetrii,
- P'' oznacza obraz punktu P' w OR-symetrii,
- P''' oznacza obraz punktu P'' w OR-symetrii,
- P(j) oznacza obraz punktu P(j-1) w OR-symetrii, czyli na przykład P(3) = P'''.
Ćwiczenie 1. Uzupełnij.
a) Jeśli P ![]() o(O, R/3), to P'
o(O, R/3), to P' ![]() . . . . . ..
. . . . . ..
b) Jeśli P ![]() o(O, 5/4.R), to P'
o(O, 5/4.R), to P' ![]() . . . . . ..
. . . . . ..
c) Jeśli P ![]() o(O, 9/4.R), to P'
o(O, 9/4.R), to P' ![]() . . . . . ..
. . . . . ..
d) Keśli P ![]() o(O, 9/4.R), to P''
o(O, 9/4.R), to P'' ![]() . . . . . ..
. . . . . ..
e) Jeśli P ![]() o(O, 9/4.R), to P'''
o(O, 9/4.R), to P''' ![]() . . . . . ..
. . . . . ..
f) P' = P wtedy i tylko wtedy, gdy P . . . . . ..
g) P' = O wtedy i tylko wtedy, gdy P . . . . . ..
h) P'' = O wtedy i tylko wtedy, gdy P . . . . . ..
i) P''' = O wtedy i tylko wtedy, gdy P . . . . . ..
j*) P(j) = O wtedy i tylko wtedy, gdy P . . . . . ..
k) P'' = P' wtedy i tylko wtedy, gdy P . . . . . ..
l) P''' = P'' wtedy i tylko wtedy, gdy P . . . . . ..
m*) P(m+1) = P(m) wtedy i tylko wtedy, gdy P . . . . . ..
n) Jeśli odległość P, O > . . . . . ., to odległość P, P'' jest równa 2R.
Nietrudno sprawdzić, że jeśli punkt P leży we wnętrzu koła k(O, R) i jest różny od O, to obrazem odcinka PPm jest odcinek PmP'. Na ogół jednak obrazami odcinków w OR-symetrii nie są odcinki.
Spróbuj odgadnąć, jak wyglądają obrazy odcinków ST, AB, BC, CA, przedstawionych na rysunku poniżej.
(Aby uzyskać podpowiedź, przesuwaj punkty Q i D. Ciekawe kształty otrzymasz, gdy A, B, C ustawisz w wierzchołkach trójkąta opisanego na okręgu m).
Obrazy odcinków przypominają łuki okręgów, ale nimi nie są.
Zamiast odcinka zbadamy dokładniej obraz prostej k w OR-symetrii.
Przyjmijmy, że QO oznacza odbicie Q względem punktu O.
Zauważ, że odległość Q'QO = 2R. Dlaczego?
Gdy Q przebiega prostą k, to QO przebiega prostą kO będącą odbiciem prostej k względem punktu O.
Zatem gdy QO przebiega prostą kO, to punkt Q' jest 'cofnięciem' punktu QO w stronę O o 2R.
Zatem Q' przebiega linię będącą 'cofnięciem' prostej kO o 2R w stronę punktu O.
Taka linia nosi nazwę konchoidy Nikodemesa prostej kO.
Zatem obrazami odcinków w OR-symetrii są fragmenty konchoid Nikodemesa.
Wyprowadzimy teraz wzór opisujący obraz k' prostej k przedstawionej na rysunku, czyli wzór konchoidy Nikodemesa tej prostej.
Niech P należy do prostej k, czyli P=(R, a.P) dla pewnej liczby a.
Ponieważ P' i P leżą na prostej przechodzącej przez O, współrzędne punktu P'=(x', y') spełniają zależność: y' = a.x' (to samo a, co poprzednio).
Ponadto fakt, że środek odcinka P'P leży na okręgu, można zapisać wzorem:
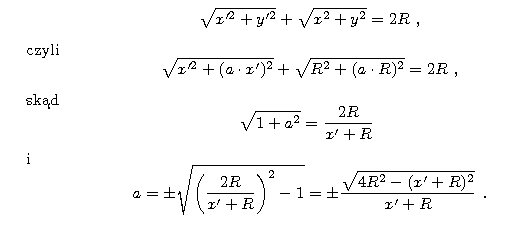
Ponieważ y' = a.x',
albo
A jak wyglądają obrazy okręgów w OR-symetrii?
Obrazami okręgów o środku w punkcie O są oczywiście okręgi o środku w O (lub sam punkt O).
Ciekawsze są jednak obrazy innych okręgów. Zobacz.
Podobnie jak dla prostych, obrazy okręgów są 'cofnięciami' odbitych okręgów. Tworzą linie zwane konchoidami okręgu (szczegóły pomijamy).
Zobacz jeszcze, jakie dziwaczne kształty może mieć konchoida brzegu kwadratu. Są to złączenia fragmentów czterech konchoid Nikomedesa.
O dalszych przygodach Karola Omyłka z przekształceniami możesz przeczytać w artykule o emsymetrii.




