Topologia

Data ostatniej modyfikacji:
2008-07-22

Odcinek jest kwadratem

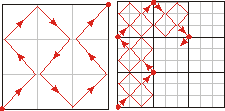Dokładniej mówiąc, istnieje ciągłe odwzorowanie odcinka na kwadrat. Ciągłość oznaczą, że odcinek może być rozciągany i wyginany, ale nie może zostać w tym odwzorowaniu rozerwany. Odwzorowanie będzie "na", jeśli odcinek przeprowadzimy przez każdy punkt kwadratu. Przykłady takich odwzorowań znaleziono dopiero w XIX w. Jeden z nich prezentujemy obok. Są to kolejne 2 kroki konstrukcji. Całe odwzorowanie powstaje, gdy będziemy powtarzać tę procedurę w nieskończoność.

Dodaj komentarz

Nie rozumiem czegoś

analfabetamatematyczny (niezweryfikowany), niedziela, 15/02/2009 - 23:13

Chyba się pogubiłem. Czy to rozciąganie i wyginanie, ale bez rozerwania, to nie jest homeomorfizm? A jeśli właśnie o to chodzi, to czemu tutaj jest napisane, że to ciągłość? Więc ciągłość to to samo co homeomorfizm?

I czy jeśli będziemy powtarzać to w nieskończoność, czy całość nie będzie tylko dążyć do zamierzonego celu, ale nim się nie stanie?

Dziękuję za odpowiedź z góry, bo naprawdę się pogubiłem, ale to zapewne ze względu na niedouczenie. Pozdrawiam.

Odpowiedz

To nie homeomorfizm

redakcja (niezweryfikowany), piątek, 20/02/2009 - 10:12

To odwzorowanie nie jest homeomorfizmem (zatem rozumowanie jest raczej sofizmatem niz paradoksem).

Homeomorfizm musi być ciągły "w obie strony" (tzn. ma być funkcją ciągłą i funkcję odwrotną też ma mieć ciągłą). Oznacza to, że odwzorowanie nie tylko nie może nic rozrywać, ale też nie może nic sklejać (bo wtedy odwzorowanie odwrotne musi to, co zostało sklejone - rozerwać, a więc nie będzie ciągłe). A w tym przykładzie sporo punktów odcinka się skleja. Zatem kwadrat jest ciągłym obrazem odcinka, ale nie jest z nim homeomorficzny (czyli nie są tym samym).

Odcinek przybliża coraz lepiej kwadrat, aż (w granicy) staje się tym kwadratem. To przekształcenie graniczne jest dobrze określone i to właśnie ono przekształca odcinek na kwadrat.

Odpowiedz

Nieistnienie takiego homeomorfizmu można uzasadnić tak

Anonimowy (niezweryfikowany), poniedziałek, 26/04/2010 - 16:32

Przypuśćmy, że istnieje homeomorfizm odcinka na kwadrat. Wówczas obrazem odcinka z usuniętym jednym punktem wewnętrznym w tym odwzorowaniu jest kwadrat z usuniętym jednym punktem. Jednak kwadrat z usuniętym jednym punktem jest zbiorem spójnym, zaś odcinek z usuniętym punktem wewnętrznym nie jest zbiorem spójnym. Czyli odwzorowanie odwrotne nie może być ciągłe. Sprzeczność.