Tekst został napisany w oparciu o arkusz kalkulacyjny MS Excel 2013. Inne wersje Excela mogą się nieznacznie różnić od prezentowanej.
W poniższej tabeli przedstawiono informacje o kilku kandydatach ubiegających się o przyjęcie na studia. W kolumnie "Pow. 20 tys." litera T oznacza "tak", czyli że kandydat mieszka w miejscowości liczącej ponad 20 000 mieszkańców, a litera N oznacza "nie", czyli że mieszka w mniejszej miejscowości. W kolumnie "J. polski R" lub "Matematyka R" litera T oznacza, że kandydat zdawał maturę z języka polskiego lub z matematyki na poziomie rozszerzonym, a litera N - że zdawał ją na poziomie podstawowym. W kolumnach "J. polski" i "Matematyka" podano procentowy wynik kandydata na maturze z danego przedmiotu (zdawanej na takim poziomie, jaki jest zaznaczony we wcześniejszych kolumnach).
| Imię | Nazwisko | Płeć | Województwo | Pow. 20 tys. | J. polski R | Matematyka R | J. polski | Matematyka |
| Feliks | Iwaszko | M | lubelskie | T | T | T | 71 | 68 |
| Sławomir | Nawrat | M | dolnośląskie | T | N | T | 64 | 98 |
| Hubert | Okrasa | M | dolnośląskie | N | N | T | 67 | 52 |
| Katarzyna | Śmiech | K | lubelskie | T | N | T | 69 | 49 |
Kiedy widzimy te dane, od razu nasuwają się różne pytania: Ile kobiet wzięło udział w rekrutacji? Z jakiego województwa pochodzi najwięcej kandydatów? Jaka część kandydatów zdawała maturę z matematyki na poziomie rozszerzonym? A jaka część zdawała maturę z obu przedmiotów na poziomie rozszerzonym? Czy średni wynik matury jest wyższy u chłopców, czy u dziewcząt? Odpowiedzi na te pytania dają obraz sylwetki przeciętnego kandydata na studia.
Podanie odpowiedzi na wyżej postawione pytania na podstawie powyższej tabeli nie jest trudne, ale wyobraźmy sobie, co by było, gdyby tabela liczy nie kilka, a kilkaset wierszy. Trzeba by się porządnie napracować, by zliczyć kobiety, osoby z dużych miejscowości czy średnie wyników maturalnych dla każdej płci. Co wtedy zrobić?
Do takich zadań można wykorzystać arkusz kalkulacyjny, a dokładniej jego element o nazwie tabela przestawna. Jego działanie poznamy na przykładach, które zostały opracowane z użyciem następującego arkusza. Ściągnij ten plik i otwórz w Excelu, a następnie wykonaj samodzielnie opisane czynności.
Tabelę przestawną można utworzyć na podstawie tabeli, która spełnia cztery warunki:
- ma tyle samo komórek w każdym wierszu,
- ma tyle samo komórek w każdej kolumnie,
- każda kolumna ma nagłówek,
- w każdym wierszu muszą być dane dotyczące odrębnego obiektu (np. każdy wiersz to dane o innej osobie).
Tworzenie tabeli przestawnej zaczynamy od zaznaczenia obszaru komórek, na podstawie którego ta tabela przestawna ma być utworzona. W naszym pliku jest to obszar A1:I537. Następnie z karty "WSTAWIANIE" wybieramy opcję "Tabela przestawna".
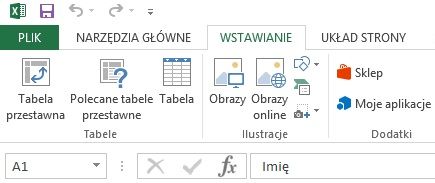
Jeśli wcześniej zaznaczyliśmy zakres komórek, zakres ów automatycznie pojawi się w oknie. Musimy jeszcze wybrać miejsce, gdzie uzyskana tabela przestawna ma się pojawić. Wybieramy "Nowy arkusz" i zatwierdzamy dokonane wybory przyciskiem "OK".
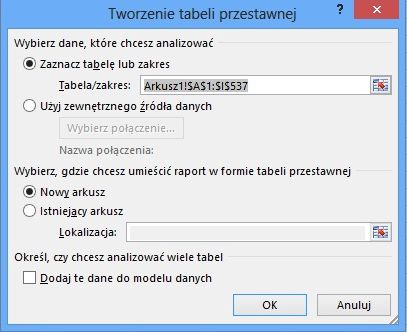
W tym momencie po prawej stronie ekranu pojawi się panel do tworzenia tabeli przestawnej. Ujrzymy w nim nagłówki wszystkich kolumn z oryginalnej tabeli w formie listy oraz cztery pola podpisane: WIERSZE, KOLUMNY, WARTOŚCI i FILTRY.
Spróbujmy znaleźć odpowiedź na pytanie, ile kobiet i ilu mężczyzn znajduje się na liście. W tym celu chwytamy kwadracik z napisem "Płeć" i upuszczamy w polu WIERSZE, a na pole WARTOŚCI upuszczamy nagłówek dowolnej kolumny. Jeśli ta kolumna zawiera liczby (np. jeśli jest to "Matematyka"), taka operacja spowoduje zsumowanie osobno punktów wszystkich kobiet i wszystkich mężczyzn, ale nie o to nam chodziło. Aby zliczyć kobiety i mężczyzn, w polu WARTOŚCI należy upuścić nagłówek jakiejś kolumny zawierającej tekst (np. kolumny "Imię").
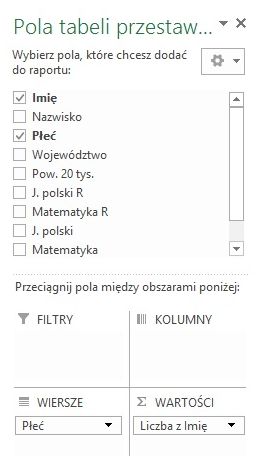
Jeśli do pola WARTOŚCI upuściliśmy jednak kolumnę "Matematyka" zawierającą liczby, to musimy rozwinąć pole "Suma z Matematyka", kliknąć "Ustawienia pola wartości" i zmienić "Suma" na "Licznik".

Łatwo się domyślić, że "Suma" powoduje dodanie liczb w kolumnie, a licznik po prostu zlicza wiersze.
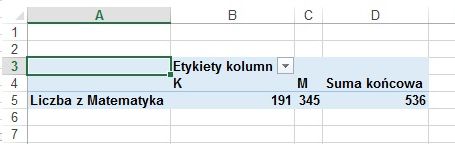
Na dwa sposoby ustaliliśmy zatem, że na liście jest 191 dziewcząt i 345 chłopców.

Ten sam efekt uzyskamy, jeśli "Płeć" przeniesiemy z pola WIERSZE do pola KOLUMNY, tylko tabela przestawna będzie teraz inaczej zorientowana.
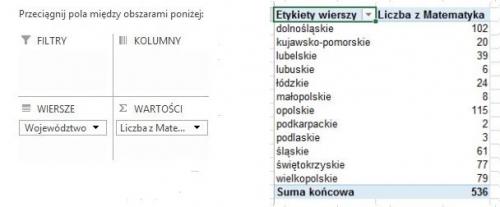
Postępując w podobny sposób, można np. sprawdzić, ile osób jest osób z województwa opolskiego, umieszczając "Województwo" w polu WIERSZE.
Jeśli chcemy edytować stworzoną już tabelę przestawną, klikamy na nią i wówczas otwiera się panel boczny. Jeśli chcemy ją zapisać i pracować z nową tabelą przestawną, wystarczy stworzyć nową tabelę w nowym arkuszu.
Jeśli chcemy się dowiedzieć, jaki był średni wynik matury z matematyki dla każdej z płci, to umieszczamy "Płeć" w polu WIERSZE, a "Matematyka" w polu WARTOŚCI. Musimy jeszcze rozwinąć napis "Suma z Matematyka", kliknąć "Ustawienia pola wartości" i domyślne "Suma" zamienić na "Średnia". Należy zwrócić uwagę na niefortunny napis "Suma końcowa" u dołu tabeli. Skoro w tabeli są zliczane średnie, to i w ostatnim wierszu będziemy mieli średnią, tym razem bez podziału na płeć.

Za pomocą tabeli przestawnej możemy też zestawić kilka cech. Jeśli chcemy zestawić dwie cechy, jedną z nich umieszczamy w polu WIERSZE, drugą w polu KOLUMNY. Na przykład jeśli chcemy się dowiedzieć, ile wśród kandydatów było chłopców a ile dziewcząt z danego województwa, to umieszczamy "Województwo" w polu WIERSZE, a "Płeć" w polu KOLUMNY. W polu WARTOŚCI umieszczamy dowolną kolumnę, byleby pojawił się w niej "Licznik". Oczywiście "Województwo" i "Płeć" możemy zamienić miejscami, ale tabela może okazać się wtedy mało czytelna. Możemy też dwie cechy umieścić jedna pod drugą w polu WIERSZE (bądź w polu KOLUMNY). W zależności od tego, która cecha będzie wyżej, uzyskamy inny wygląd tabeli.
Postępując podobnie, możemy np. obliczyć średni wynik z matury na poziomie podstawowym i rozszerzonym dla danej płci. Możemy też przekonać się, ile osób zdawało jednocześnie maturę z języka polskiego i matematyki na poziomie rozszerzonym, ile zdawało oba te przedmioty na poziomie podstawowym, lub też każdy z przedmiotów na innym poziomie.
Oczywiście niniejszy tekst nie wyczerpuje wszystkich możliwości, jakie dają tabele przestawne. W kolejnych odcinkach poznamy ich więcej.
Tabele przestawne występują także w arkuszach kalkulacyjnych OpenOffice Calc i LibreOffice Calc (w starszych wersjach zwane są pilotem danych) i nie tracą tam nic ze swej funkcjonalności w stosunku do Excela. Użytkowników tych programów zachęcamy do zapoznania się z tym, jak tabele przestawne są w nich obsługiwane.
Na podstawie danych z arkusza kalkulacyjnego, który został omówiony w ramach miniwykładu, utwórz tabele przestawne, które pozwolą odpowiedzieć na następujące pytania:
Zad. 1. Gdzie średni wynik z matury z języka polskiego (liczony dla obu poziomów łącznie) jest wyższy: wśród uczniów pochodzących z miejscowości do 20 000 mieszkańców, czy też z większych miejscowości?
Zad. 2. Gdzie średni wynik z matury z języka polskiego na poziomie podstawowym jest wyższy: wśród uczniów pochodzących z miejscowości do 20 000 mieszkańców, czy też z większych miejscowości?
Zad. 3. Ile wynosi liczba kandydatów z miejscowości liczących do 20 000 mieszkańców, którzy zdawali maturę z języka polskiego na poziomie rozszerzonym?
Zad. 4. Które województwo wypadło najlepiej pod względem wyniku maturalnego z matematyki na poziomie rozszerzonym? (Wynik województwa będziemy mierzyli średnią wyników pochodzących z niego kandydatów).
Zad. 5. Czy prawdą jest, że wśród wybierających maturę z języka polskiego na poziomie rozszerzonym, przeważają dziewczęta, a wśród wybierających maturę z matematyki na poziomie rozszerzonym chłopcy?
Zad. 6. Ile wśród kandydatów jest kobiet, które zdawały maturę z języka polskiego i z matematyki na poziomie rozszerzonym?
Jako rozwiązanie prześlij odpowiedzi na powyższe pytania wraz z arkuszem kalkulacyjnym, w którym będą się znajdowały tabele przestawne, na podstawie których można udzielić odpowiedzi. Każda tabela przestawna powinna się znajdować w osobnej karcie, a karty powinny być podpisane numerami pytań. Odpowiedź na każde pytanie (wraz z potwierdzającą ją tabelą przestawną) warta jest 0,5 punktu.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Zad. 6 | Suma |
| Jakub Ptak | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
| Adam Stachelek | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 3 punkty
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 3 punkty
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Zad. 6 | Suma |
| Mateusz Winiarski | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Mateusz Winiarski (Gimnazjum Dwujęzyczne im. Mikołaja Kopernika w Krośnie) - 3 punkty
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Zad. 6 | Suma |
| Marcin Kuna | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
| Joanna Lisiowska | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
| Wojciech Wiśniewski | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Marcin Kuna (VII Liceum Ogólnokształcące im. K. K. Baczyńskiego we Wrocławiu) - 3 punkty
Joanna Lisiowska (XXI Liceum Ogólnokształcące im. H. Kołłątaja w Warszawie) - 3 punkty
Wojciech Wiśniewski (I Liceum Ogólnokształcące im. W. Kętrzyńskiego w Giżycku) - 3 punkty
Wyniki znajdują się w tym pliku. Kolorem zielonym zaznaczono liczby, które wzięto pod uwagę przy formułowaniu odpowiedzi.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


