W poprzednim roku szkolnym zagadnienia, jakim poświęcone były kolejne miniwykłady w ramach ligi zadaniowej z analizy danych, skupiały się na pytaniu: jak opisać zbiór danych, które zgromadziliśmy? Można tego dokonać z pomocą pewnych charakterystyk liczbowych zwanych statystykami opisowymi (średnia, mediana, wariancja, współczynnik skośności, kwartyle). Można też przedstawić dane na rysunku (histogram, wykres pudełkowy). Właśnie od obiczenia statystyk testowych i sporządzenia różnych wykresów zazwyczaj rozpoczyna się każda analiza danych, bowiem osoba, która ma z danymi pracować, najpierw chce się zorientować ogólnie w ich strukturze, nim zacznie poszukiwać odpowiedzi na bardziej złożone pytania. Dział statystyki, który zajmuje się właśnie takim opisem czy też ilustracją zbioru danych, nazywa się statystyką opisową.
Kontynuując nasze rozważania na temat analizy danych, od "oglądania" danych przechodzimy do bardziej złożonego matematycznego ich opisu. Ponieważ statystyka matematyczna obficie czerpie z rachunku prawdopodobieństwa, musimy wzbogacić swoją wiedzę z tej właśnie dyscypliny matematycznej. Najbliższe odcinki ligi będą zatem poświęcone wybranym zagadnieniom rachunku prawdopodobieństwa.
Tych, którzy z żadnymi zagadnieniami rachunku prawdopodobieństwa nie zetknęli się jeszcze w szkole, pragnę uspokoić; liga zadaniowa z analizy danych będzie tu zupełnie samowystarczalna tzn. dla zrozumienia kolejnych odcinków nie będzie w ogóle konieczna znajomość tych zagadnień z rachunku prawdopodobieństwa, o których mówi się w szkole. Jednocześnie pragnę uspokoić tych, którzy sądzą, że znajomość szkolnego rachunku prawdopodobieństwa będzie dla kogoś ułatwieniem; w ramach ligi nie będziemy poruszali szkolnych tematów, a dla każdego ucznia każde zagadnienie będzie nowe (i - mam nadzieję - ciekawe). A zatem... do dzieła!
Skoro mamy się zajmować prawdopodobieństwem, na początku wypadałoby zdefiniować to pojęcie prawdopodobieństwa. Niestety formalna definicja tego matematycznego obiektu jest trudna i jej przedstawienie zdecydowanie wykracza poza możliwości naszego cyklu. Z drugiej strony uproszczona definicja, którą poznaje się w liceum (nazywana formalnie tzw. klasyczną definicją prawdopodobieństwa) nie będzie dla nas użyteczna. Dla naszych rozważań zupełnie wystarczające będzie intuicyjne rozumienie prawdopodobieństwa, tym bardziej, że słowem "prawdopodobieństwo" posługujemy się na co dzień, postrzegając jego znaczenie intuicyjnie. Aby nie być jednak zupełnie skazanymi na intuicję, możemy powiedzieć, że prawdopodobieństwo to funkcja, która każemu zdarzeniu przyporządkowuje liczbę z przedziału [0,1]. Nie będziemy precyzowali, czym w ujęciu matematycznym jest zdarzenie.Jeśli prawdopodobieństwo jakiegoś zdarzenia wynosi 0, to mówimy, że jest to zdarzenie niemożliwe. Z kolei jeśli prawdopodobieństwo jakiegoś zdarzenia wynosi 1, to mówimy, że jest to zdarzenie pewne.
Naszą przygodę z prawdopodobieństwem rozpocznijmy od prostego przykładu.
Przykład 1. Podróżny przybywa na przystanek tramwajowy. Nie ma świadomości, która jest godzina. Wie, że na tym przystanku zatrzymują się tramwaje tylko jednej linii i że kursują one co 20 minut, jednak nie wie, jak dawno temu ostatni raz przejeżdżał tramwaj. Jakie jest prawdopodobieństwo, że jeśli nie wystąpią żadne nieprzewidziane okoliczności, kolejny tramwaj nadjedzie w ciągu najbliższych 5 minut?
Rozwiązanie. Wiadomo, że kolejny tramwaj na pewno przyjedzie w ciągu najbliższych 20 minut. Wszystkie możliwe momenty przybycia tramwaju można więc zobrazować za pomocą przedziału [0,20]. Pytamy o prawdopodobieństwo przyjazdu tramwaju w ciągu najbliższych 5 minut, a zatem momenty przybycia tramwaju, które nas interesują, mogą być zobrazowane poprzez przedział [0,5]. Wówczas prawdopodobieństwo rozważanego zdarzenia będzie ilorazem długości przedziału [0,5] i przedziału [0,20] a więc będzie równe (5-0):(20-0)=5/20=1/4.

Oczywiście w naszych rozważaniach dokonujemy uproszczenia polegającego na tym, że w rzeczywistości gdyby tramwaj ledwo co odjechał, podróżny przybywszy na przystanek, najprawdopodobniej jeszcze zobaczyłby odjeżdżający tramwaj, a więc wiedziałby, kiedy przyjedzie następny. Na tym przykładzie widzimy, że prawdopodobieństwo wyznaczamy zawsze w odniesieniu do konkretnych informacji, jakie posiadamy. Prawdopodobieństwo jest więc w pewnym sensie obliczane zawsze z perspektywy konkretnej osoby posiadającej dany zestaw informacji. Gdybyśmy bowiem na opisaną sytuację patrzyli z punktu widzenia motorniczego, który prowadzi tramwaj, jakiego spodziewa się nasz podróżny, wszystko byłoby w miarę jednoznacznie określone, motorniczy bowiem wie, czy na danym przystanku znajdzie się w określonym czasie, czy nie (w oparciu o rozkład jazdy, nie uwzględniamy żadnych losowych wypadków). Z perspektywy motorniczego przybycie na określony przystanek w ciągu najbliższych pięciu minut byłoby albo zdarzeniem pewnym albo niemożliwym. Ba, wystarczyłoby, że nasz podróżny mógłby sprawdzić aktualną godzinę! Wówczas rzut oka na rozkład jazdy eksponowany na przystanku pozwoliłby mu zorientować się, czy to, że tramwaj nadjedzie w ciągu najbliższych 5 minut, jest pewne czy niemożliwe. Podróżny jednak nie zna aktualnej godziny.
Ujęcie prawdopodobieństwa prezentowane w przykładzie nosi nazwę prawdopodobieństwa geometrycznego, bowiem poszczególne zdarzenia zostały tu zilustrowane jako odcinki a prawdopodobieństwo jako iloraz ich długości. Niejeden czytelnik może jednak powiedzieć sceptycznie, że do tak prostego zagadnienia nie potrzebna była żadna geometryczna ilustracja. Toteż rozważań o tramwajach ciąg dalszy.
Przykład 2. Podobnie jak w poprzednim przykładzie pasażer przybywa na przystanek tramwajowy, nie znając godziny i nie wiedząc, kiedy odjechał poprzedni tramwaj. Wie jednak, że na przystanku zatrzymują się tramwaje dwóch linii odjeżdżające co 20 minut, nie wie jednak, jaka jest różnica czasu między odjazdami tramwajów tych dwóch linii. Jest mu obojętne, do której linii wsiądzie. Jakie jest prawdopodobieństwo, że odjedzie w ciągu najbliższych 5 minut?
Rozwiązanie. Ponieważ oba tramwaje powinny przyjechać w ciągu najbliższych 20 minut, ilustracją całej sytuacji będzie kwadrat o wierzchołkach w punktach (0,0), (20,0), (20,20) i (0,20). Dwie współrzędne każdego punktu tego kwadratu będą oznaczały, za ile minut mogą przyjechać tramwaje dwóch linii (np. punkt (7,12) jest ilustracją sytuacji, gdy tramwaj jednej linii przybywa za 7 minut a tramwaj drugiej linii za 12 minut).

Pole kwadratu wynosi 202=400. Z kolei sytuację, w której ten tramwaj, na który czas oczekiwania jest krótszy, przyjedzie w ciągu najbliższych 5 minut, ilustruje zaznaczony na szaro wielokąt. Jego pole wynosi 175. Wobec tego prawdopodobieństwo tego, że najwcześniejszy tramwaj nadjedzie w ciągu 5 minut, wynosi 175/400=7/16.
I trzecia odsłona zadań z tramwajami.
Przykład 3. Dwóch kolegów z pracy mieszka w niewielkiej odległości od siebie i jeżdżą do pracy tramwajem, wsiadając doń na tym samym przystanku. W firmie, w której pracują, nie ma konieczności przychodzenia do pracy na określoną godzinę. Pracownik ma stawić się w pracy między godz. 8.30 a 9.30. Wobec tego każdy z dwóch kolegów jeździ do pracy tramwajem odjeżdżającym z ich przystanku między godz. 7.00 i 8.00, każdego dnia przybywając na przystanek w dowolnym momencie między tymi godzinami. Tramwaj, którym jeżdżą do pracy, odjeżdża z ich przystanku o godz. 7.00 i potem co 15 minut. Koledzy nigdy się nie umawiają, o której godzinie pojadą do pracy danego dnia, więc zdarza się, że jadą tym samym tramwajem, ale zdarza się też, że się rozmijają. Oblicz prawdopodobieństwo, że koledzy jadą do pracy tym samym tramwajem.
Rozwiązanie. Tym razem ilustracją dla opisanej sytuacji będzie kwadrat o wierzchołkach w punktach (0,0), (60,0), (60,60) i (0,60). Współrzędne każdego punktu w tym kwadracie oznaczają liczbę minut po godz. 7.00, gdy każdy z dwóch kolegów przybywa na przystanek (np. punkt (32,48) oznacza sytuację, gdy jeden z kolegów przybywa na przystanek o godz. 7.32 a drugi o godz. 7.48).

Pole tego kwadratu wynosi 602=3600. Jeśli obaj koledzy przyjdą na przystanek w tym samym kwadransie, to pojadą do pracy tym samym tramwajem, w przeciwnym razie pojadą różnymi tramwajami. W takim razie sytuację, gdy obaj koledzy jadą jednym tramwajem, ilustrują cztery zaciemnione kwadraty. Suma pól tych kwadratów wynosi 4·152=900. Wobec tego prawdopodobieństwo tego, że obaj koledzy jadą jednym tramwajem, wynosi 900/3600=1/4.
[koniec wykładu dla gimnazjalistów]
Jednym z ciekawych zastosowań prawdopodobieństwa geometrycznego może być... znalezienie wymiernego przybliżenia liczby π. Rozważmy kwadrat o wierzchołkach w punktach (-1,-1), (1,-1), (1,1) i (-1,1) oraz koło o środku w punkcie (0,0) i promieniu 1 jak na rysunku.
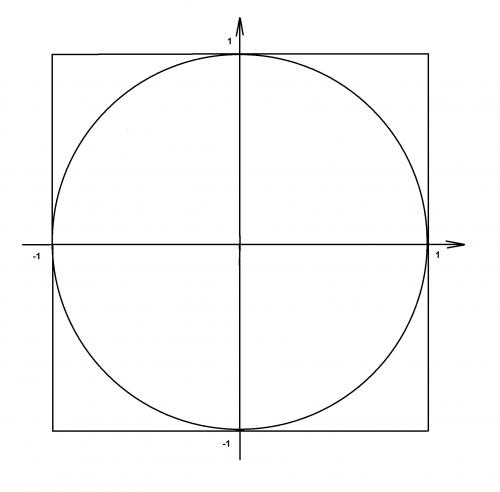
Gdybyśmy zrobili doświadczenie polegające na tym, że wybieralibyśmy losowo punkt z kwadratu, to prawdopodobieństwo, że wylosowany punkt należałby do koła, byłoby, zgodnie z koncepcją prawdopodobieństwa geometrycznego, równe stosunkowi pola koła do pola kwadratu. Ponieważ pole kwadratu jest równe 22=4 a pole koła π·12=π, więc prawdopodobieństwo wylosowania punktu z koła wynosiłoby π/4. Gdybyśmy jakoś przybliżyli to prawdopodobieństwo, wystarczyłoby pomnożyć je przez 4, by uzyskać przybliżenie liczby π.
Prawdopodobieństwo wylosowania punktu z koła przy losowaniu z kwadratu najprościej jest oszacować, losując pewną liczbę punktów z kwadratu i sprawdzając, ile spośród nich należy do koła, a następnie dzieląc liczbę punktów należących do koła przez liczbę wszystkich wylosowanych punktów.
Problemem pozostaje jeszcze losowanie punktów z kwadratu. Nim do powszechnego użytku weszły komputery, losowanie takie mogłoby się odbywać np. za pomocą kostki takiej jak na rysunku.

Jeśli chciałoby się losować liczby dokładnością np. do czterech miejsc po przecinku, wówczas należałoby rzucić kostką cztery razy i zanotować poszczególne wyniki jako kolejne cyfry po przecinku (cyfra jedności wynosi 0). Ponieważ współrzędne rozważanego kwadratu są liczbami z przedziału (-1,1), należałoby jeszcze wylosować znak liczby np. rzucając monetą. W ten sposób za pomocą czterech rzutów kostką i jednego rzutu monetą otrzymalibyśmy jedną liczbę. Drugie takie losowanie pozwoliłoby nam uzyskać drugą liczbę a więc jeden punkt z kwadratu (jako dwie współrzędne). Intuicja podpowiada nam, że im więcej punktów byśmy wylosowali, tym nasze przybliżenie liczby pi byłoby dokładniejsze.
Pozwoliłem sobie na przeprowadzenie opisanego wyżej eksperymentu, jednak do losowania liczb użyłem komputera. Wylosowałem 20 punktów. Następnie dla każdego z nich sprawdziłem, czy należy do koła (tzn. czy jego współrzędne spełniają nierówność x2+y2 ≤ 1 wynikającą z twierdzenia Pitagorasa).
| lp. | x | y | x2+y2 | Czy x2+y2 ≤ 1 ? |
| 1 | 0,6107 | -0,1944 | 0,4107 | TAK |
| 2 | -0,9688 | 0,5904 | 1,2871 | NIE |
| 3 | 0,1238 | -0,7519 | 0,5806 | TAK |
| 4 | 0,8122 | -0,2423 | 0,7183 | TAK |
| 5 | -0,9585 | 0,7306 | 1,4524 | NIE |
| 6 | 0,7356 | -0,2288 | 0,5934 | TAK |
| 7 | 0,5346 | -0,5704 | 0,6111 | TAK |
| 8 | -0,6544 | -0,7607 | 1,0069 | NIE |
| 9 | -0,9123 | 0,8340 | 1,5278 | NIE |
| 10 | -0,5303 | -0,6430 | 0,6946 | TAK |
| 11 | 0,6369 | -0,3540 | 0,5309 | TAK |
| 12 | 0,8139 | -0,9679 | 1,5992 | NIE |
| 13 | 0,5587 | 0,5520 | 0,6168 | TAK |
| 14 | -0,4711 | -0,7668 | 0,8099 | TAK |
| 15 | -0,0735 | 0,5497 | 0,3075 | TAK |
| 16 | 0,5624 | -0,8190 | 0,9870 | TAK |
| 17 | 0,0775 | -0,4574 | 0,2152 | TAK |
| 18 | -0,1891 | -0,1356 | 0,0541 | TAK |
| 19 | 0,9787 | 0,7995 | 1,5970 | NIE |
| 20 | -0,6449 | 0,9702 | 1,3571 | NIE |
Spośród 20 wylosowanych punktów 16 należy do koła, a zatem prawdopodobieństwo wylosowania punktu z koła szacujemy na 16/20=0,8. Wobec tego pi wynosi w przybliżeniu 0,8·4=3,2. Oczywiście trzeba pamiętać, że wynik zależy od tego, jakie punkty zdarzy się nam wylosować.
Zad. 1. Monetę jednogroszową (średnica: 15,5 mm) rzucono losowo na szachownicę, której każde z pól jest kwadratem o boku 5,5 cm. Zakładamy, że moneta upadła na obszar wyznaczony przez pola. Jakie jest prawdopodobieństwo, że znajduje się ona w całości w jednym z pól?
Zad. 2. Kilka lat temu, gdy w użyciu były jeszcze kasety magnetofonowe, dziennikarz wybrał się na wywiad i zabrał ze sobą dyktafon i kasetę ze 120-minutową taśmą (tzn. jedna strona kasety mieściła nagranie 60 minut). Nagranie wywiadu na kasecie zajmowało na taśmie czas dokładnie od 21 do 34 minuty ustalonej strony kasety. Potem dziennikarz nagrywał na tej samej stronie kasety jeszcze inne materiały. Po powrocie do domu przesłuchiwał różne fragmenty nagrań z tej kasety, przewijając ją to w przód, to w tył. W końcu, nie zdając sobie sprawy, w którym momencie taśmy jest, postanowił przewinąć taśmę do początku, wcisnął więc przycisk i poszedł do kuchni. Wrócił po 15 minutach z przerażeniem odkrył, że zamiast przycisku przewijania wcisnął przycisk nagrywania. Natychmiast wyłączył nagrywanie. Niestety w ten sposób skasował 15 minut z materiału, jaki był zarejestrowany na jej samej stronie kasety co wywiad. Oblicz prawdopodobieństwo, że nie skasowało się nic z wywiadu, jaki tego dnia przeprowadzał dziennikarz.
Jeśli uczestnicy ligi mają trudność ze zrozumieniem treści tego zadania, bo nigdy nie mieli do czynienia z magnetofonem, niech poproszą o wyjaśnienie rodziców. :)
Zad. 3. Z przedziału (0,1) losujemy liczbę a a następnie niezależnie od niej z przedziału (-1,1) losujemy liczbę b. Jakie jest prawdopodobieństwo, że miejsce zerowe funkcji y = ax+b jest dodatnie?
Zad. 1. Ala i Jacek - matematycy - umówili się w kawiarni, ale nie umówili się co do konkretnej godziny. Ustalili tylko, że każde z nich przyjdzie do kawiarni w dowolnym momencie między godziną 12.00 a 13.00 i jeśli nie spotka wewnątrz drugiego, poczeka 20 minut (lub krócej, jeśli wybije już 13.00) i jeśli się nie doczeka na drugie, wyjdzie. Jakie jest prawdopodobieństwo, że Ala i Jacek nie rozminą się ale spotkają się w kawiarni?
Zad. 2. Monetę o średnicy d upuszczono na posadzkę wyłożoną kafelkami o wzorze jak na zdjęciu, gdzie ramię każdego spośród białych i czarnych trójkątów prostokątnych równoramiennych ma długość a. Jakie jest prawdopodobieństwo, że moneta upadnie w taki sposób, że będzie się w całości znajdowała wewnątrz jednego białego lub czarnego trójkąta? Zakładamy, że posadzkę położono bez fug i że trójkąty są na tyle duże, że moneta zmieści się w całości w jednym z nich.

Zad. 3. Z przedziału (-3,3) losujemy liczbę m. Oblicz prawdopodobieństwo, że trójmian kwadratowy x2+2mx+m+2 ma dwa pierwiastki.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Dawid Konieczko | 0 | 0 | 0 | 0 |
| Joanna Lisiowska | 1 | 1 | 1 | 3 |
| Jakub Ptak | 1 | 0 | 1 | 2 |
| Adam Stachelek | 0,5 | 1 | 1 | 2,5 |
Klasyfikacja generalna:
Joanna Lisiowska (Katolicki Zespół Edukacyjny im. Piotr Skargi w Warszawie) - 3 punkty
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 2,5 punktu
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 2 punkty
Dawid Konieczko (Społeczne Gimnazjum z Oddziałami Dwujęzycznymi w Szprotawie) - 0 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Witold Barcz | 0 | 0 | 1 | 1 |
| Daria Bumażnik | 0 | 0 | 1 | 1 |
| Tomasz Stempniak | 1 | 1 | 1 | 3 |
Klasyfikacja generalna:
Tomasz Stempniak (I Liceum Ogólnokształcące w Ostrowie Wielkopolskim ) - 3 punkty
Witold Barcz (Zespół Szkół Elektryczno-Mechanicznych w Nowym Sączu) - 1 punkt
Daria Bumażnik (II Liceum Ogólnokształcące im. C. K. Norwida w Jeleniej Górze) - 1 punkt
Zad. 1. Wystarczy rozważyć tylko jedno pole szachownicy jak na rysunku. Będziemy rozpatrywali punkty, w których może upaść środek monety. Punktem, gdzie upadnie środek monety, może być dowolny punkt pola szachownicy. Pole powierzchni pola szachownicy wynosi (55 mm)2= 3025 mm2. Jeśli chcemy, aby moneta znalazła się w całości w jednym polu szachownicy, to jej środek musi upaść w punkcie należącym do zaznaczonego na czerwono kwadratu, którego bok jest krótszy od boku pola szachownicy o długość średnicy monety. Pole powierzchni takiego kwadratu wynosi zatem (55 mm - 15,5 mm)2=(39,5 mm)2=1560,25 mm2. W takim razie prawdopodobieństwo tego, że moneta znajdzie się w całości w jednym z pól, wynosi 1560,25 mm2/3025 mm2 = 6241/12100 ≈ 0.52.

Zad. 2. Będziemy rozważali miejsce na taśmie, w którym rozpoczęło się omyłkowe nagrywanie. Ponieważ całe omyłkowe 15-minutowe nagranie zmieściło się na taśmie (dziennikarz wyłączył nagrywanie) a na jednej stronie taśmy mieści się 60 minut, moment rozpoczęcia nagrywania musiał wystąpić do 45 minuty. Wszystkie możliwe sytuacje będziemy zatem utożsamiali z przedziałem [0,45], którego długość wynosi 45-0=45. Jeśli żaden fragment wywiadu nie został skasowany, omyłkowe nagranie mogło się rozpocząć do 6 minuty (od 6 do 21 minuty pozostaje 15 minut) lub po 34 minucie. Sytuację, w której nic z wywiadu się nie skasowało, możemy utożsamić ze zbiorem $[0,6]\cup[34,45]$. Jest on sumą rozłącznych przedziałów, a suma ich długości wynosi (6-0)+(45-34)=6+11=17. Wobec tego prawdopodobieństwo tego, że nie skasowało się nic z wywiadu, wynosi 17/45 .
Zad. 3. Skoro a > 0 (gdyż a losujemy z przedziału (0,1)), funkcja y = ax+b ma jedno miejsce zerowe i wynosi ono - b/a. Widzimy, że przy poczynionych założeniach - b/a > 0 wtedy i tylko wtedy, gdy b < 0. Liczba b została wylosowana z przedziału (-1,1) o długości 1-(-1)=1+1=2. Nakładając na $b\in (-1,1)$ ograniczenie b < 0, otrzymujemy, że $b\in (-1,0)$. Długość tego przedziału wynosi 0-(-1)=0+1=1. W takim razie prawdopodobieństwo, że miejsce zerowe funkcji y = ax+b jest dodatnie, wynosi ½.
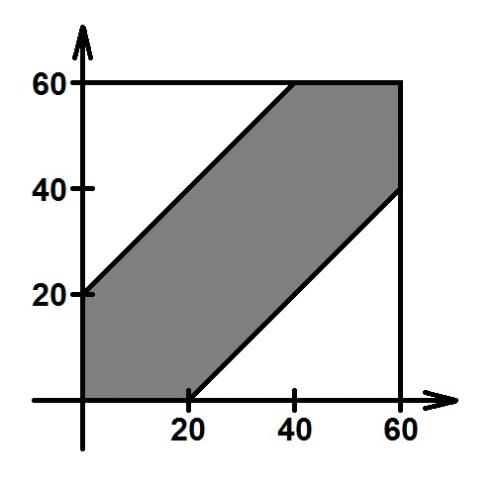
Zad. 1. Niech x oznacza czas liczony w minutach począwszy od godz. 13.00 do momentu, gdy do restauracji przychodzi Ala zaś y - czas liczony w minutach począwszy od godz. 13.00 do momentu, gdy do restauracji przychodzi Jacek. Skoro każde z nich przybywa do restauracji do godz. 14.00, zarówno x jak i y należą do przedziału [0,60]. W takim razie punkt (x,y) należy do kwadratu o wierzchołkach w punktach (0,0), (60,0), (60,60) i (0,60). Pole tego kwadratu wynosi 602 = 3600. Jeśli Ala i Jacek mają się spotkać, a każde z nich czeka w restauracji jedynie 20 minut, to |y-x| ≤ 20 czyli -20 ≤ y-x ≤ 20, a więc x-20 ≤ y ≤ x+20. Oznacza to, że wówczas punkt (x,y) leży w tej części wcześniej wspomnianego kwadratu, która znajduje się pomiędzy prostymi o równaniach y = x-20 i y = x+20 a więc w szarym obszarze na rysunku. Pole tego obszaru można łatwo obliczyć, odejmując od pola kwadratu pola dwóch białych trójkątów prostokątnych równoramiennych o długościach przyprostokątnych 40. Pole szarego obszaru wynosi zatem 3600-2·½·402 = 3600-1600 = 2000. Wobec tego prawdopodobieństwo tego, że Ala i Jacek spotkają się, wynosi 2000/3600 = 5/9.
Zad. 2. Wystarczy rozważyć tylko jeden trójkąt jak na rysunku. Będziemy rozpatrywali punkty, w których może upaść środek monety. Punktem, gdzie upadnie środek monety, może być dowolny punkt należący do trójkąta ABC. Pole trójkąta ABC wynosi ½ a2. Jeśli chcemy, aby moneta znalazła się w całości w trójkącie ABC, to jej środek musi upaść w punkcie należącym do trójkąta A'B'C', który podobnie jak trójkąt ABC jest trójkątem prostokątnym równoramiennym. Do obliczenia jego pola wystarczy znalezienie długości odcinka B'D'. Z treści zadania wynika, że ||AB|| = ||BC|| = a i ||DE|| = ||DD'|| = r/2. W oparciu o twierdzenie Pitagorasa nietrudno jest znaleźć ||BD|| i ||BB'||. Mamy zatem ||BD|| = $\frac{a \sqrt{2}}{2}$ i ||BB'|| = $\frac{d \sqrt{2}}{2}$. W takim razie ||B'D'|| = ||BD||-||BB'||-||DD'||= $\frac{a \sqrt{2}}{2} - \frac{a \sqrt{2}}{2}-\frac{d}{2}$. Pole trójkąta A'B'C' jest takie samo jak pole kwadratu o boku B'D' a zatem jest ono równe ||B'D'||2 = $(\frac{a \sqrt{2}}{2} - \frac{a \sqrt{2}}{2}-\frac{d}{2})^2 = \frac{1}{4} (a \sqrt{2}- d \sqrt{2} - d)^2$. W takim razie prawdopodobieństwo tego, że moneta będzie się znajdowała w całości w jednym z trójkątów, wynosi $\frac{\frac{1}{4} (a \sqrt{2}- d \sqrt{2} - d)^2}{\frac{1}{2}a^2}=\frac{(a \sqrt{2}- d \sqrt{2} - d)^2}{2a^2}$.

Zad. 3. Wyróżnik trójmianu kwadratowego x2+2mx+m+2 jest równy Δ = (2m)2-4(m+2) = 4m2-4(m+2) = 4(m2-m-2) = 4(m+1)(m-2). Trójmian kwadratowy ma dwa pierwiastki wtedy i tylko wtedy, gdy Δ > 0 a zatem gdy $m\in (-3,-1)\cup(2,3)$. W ten sposób otrzymaliśmy sumę rozłącznych przedziałów, których suma długości wynosi [-1-(-3)]+[2-3] = 2+1 = 3. Ponieważ długość przedziału (-3,3), z którego losujemy m, wynosi 3-(-3) = 3+3 = 6, więc prawdopodobieństwo tego, że trójmian kwadratowy x2+2mx+m+2 ma dwa pierwiastki, wynosi 3/6 = 1/2.






