Zad. 1. Jacek i Agatka na kalkulatorze prostym obliczali wartość √458,44 × √0,67.
Jacek obliczył pierwiastek z pierwszej liczby, wynik wprowadził do pamięci, potem wyliczył pierwiastek z drugiej liczby i pomnożył przez wartość wywołaną z pamięci. Otrzymał 17.5258323623.
Agatka skorzystała z rozdzielności pierwiastkowania względem mnożenia: obliczyła iloczyn liczb podpierwiastkowych i wyciągnęła z niego pierwiastek. Otrzymała 17.5258323625.
a) Skąd wzięła się różnica wyników?
b) Czyj wynik jest dokładniejszy? Dlaczego?
Zad. 2. Jakie największe pudełko (bez denka) można wykonać z blachy formatu A4, wycinając w jej narożnikach jednakowe kwadraty i lutując krawędzie? W rozwiązaniu można użyć tylko elementarnych metod (na poziomie SP) i kalkulatora lub komputera. W szczególności nie wolno używać rachunku różniczkowego. Odpowiedź podaj z dokładnością do setnych części milimetra sześciennego. Opisz w 2-3 zdaniach, swój pomysł na rozwiązanie problemu.
Zad. 3. Włoski matematyk Giuseppe Peano w 1890 roku opisał konstrukcję linii, która rysowana w sposób ciągły (bez odrywania ręki od papieru) wypełniała cały kwadrat. Tym samym pokazał, że używana wówczas definicja wymiaru nie jest formalnie poprawna - obiekt jednowymiarowy (linia) - okazał się być dwuwymiarowym (kwadratem). Po latach tego typu krzywe nazwano na jego cześć... No właśnie - jak? Jaki jest stosunek liczby wyników znalezionych po wpisaniu do wyszukiwarki terminów "krzywa Peano", "krzywa Peana" i "krzywa Peany"? Użyj jakiejś popularnej wyszukiwarki i napisz, jakiej użyłeś. Która wersja jest poprawna? Podaj link do strony internetowej, na której znajduje się ogólna reguła rozstrzygająca tę wątpliwość.
Z zadaniem 1 uczestnicy ligi nie mieli na ogół problemów. W zadaniu 2 jako poprawne oceniane były tylko rozwiązania, w których pudełko wykonane było opisaną w treści zadania metodą. Niektórzy zawodnicy podawali wynik w jednostkach kwadratowych. Nie zawsze bylo jasne, co to za wielkość, ale trudno ją uznać za miarę "wielkości pudełka". Naturalną miarą jest w tym wypadku pojemność pudełka. W zadaniu 3 zdarzały się odpowiedzi z istotną nadreprezentacją wyników "krzywa Peany". Podawane dane dotyczyły jednak stron, na których oba słowa mogły występować osobno, nie jako jeden związek frazeologiczny (wobec tego liczone były także wystąpienia rzeczownika pospolitego "peany").
Komplet 3 punktów uzyskali w tym miesiącu: Krystyna Lisiowska - redaktor z Warszawy i Andrzej Piasecki - administrator IT z Oleśnicy. Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan, uzyskała 2,75 punktu, Daria Bumażnik - uczennica II LO w Jeleniej Górze i Piotr Wróbel - inżynier z Brwinowa - otrzymali po 2,5 punktu, a Krzysztof Danielak - uczeń I LO w Jeleniej Górze - 2 pkt. Po 1,5 punktu zdobyli: Mirosław Baszczak - programista z Warszawy, Kamila Bojar - uczennica LO w Szprotawie, Anna Jakubczak - uczennica ZS nr 1 w Ostrzeszowie i Wojciech Tomiczek - inżynier z Lipowej. Pozostałym zawodnikom przyznano 1 punkt lub mniej.
Po pięciu miesiącach trwania Ligi najwięcej punktów zdobyli (na 15 możliwych):
- 14,5 - Andrzej Piasecki
- 13,75 - Marzena Wąsiewicz
- 13 - Krystyna Lisiowska, Krzysztof Danielak i Piotr Wróbel
- 12,5 - Mirosław Baszczak i Wojciech Tomiczek
- 12 - Kamila Bojar
- 11,5 - Daria Bumażnik
- 10,5 - Tomasz Skalski - student matematyki na PWr.
Gratulujemy!
Zad. 1. Różnica wyników bierze się z tego, że oba czynniki są liczbami niewymiernymi (mają nieskończone rozwinięcia dziesiętne), czyli niezależnie od wielkości wyświetlacza, kalkulator 'pamięta' je tylko w przybliżeniu. W metodzie Jacka każdy z czynników został przybliżony osobno, czyli zaokrąglenia wystąpiły w rachunku dwukrotnie. W metodzie Agatki iloczyn liczb wymiernych został obliczony w sposób dokładny, a przybliżenie pojawiło się tylko raz, podczas wyliczania pierwiastka. Błąd metody Agatki jest mniejszy. Dokładniejsze przyblizenie wyniku wynosi 17.52583236254415...
Zad. 2. Do rozwiązania zadania wystarczy znajomość wzoru na objętość prostopadłościanu i znormalizowanych wymiarów arkusza formatu A4 (297 mm × 210 mm). Można, zmieniając długość boku wycinanego kwadratu co 1 mm w zakresie od 0 do 105, obliczyć objętość pudełka w arkuszu kalkulacyjnym, a następnie użyć opcji Solvera i znaleźć komórkę o największej zawartości. Można to samo uzyskać za pomocą kalkulatora graficznego (lub dowolnego programu rysującego wykresy funkcji). Oznaczając przez x długość boku wycinanego kwadratu, narysować na przedziale [0, 105] wykres funkcji opisującej objętość otrzymanego prostopadłościanu, a następnie użyć opcji Solvera i znaleźć argument, dla którego wartość funkcji jest największa. To samo można uzyskać, używając opcji "max" w pakiecie WolframAlpha.
V(x) = x(297-2x)(210-2x)
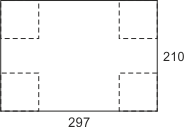
Oczywiście należy zadbać o uzyskanie wyniku gwarantującego wymaganą dokładność odczytu. Obie metody dają wynik 1128495,105 mm3 (czyli otrzymujemy pudełko o maksymalnej pojemności około 1 litra) dla wycięcia o długości boku 40,42 mm.
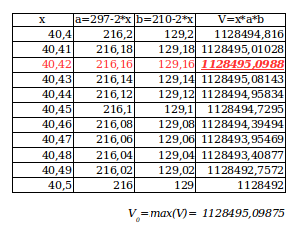
Zrzut ekranu kalkulatora graficznego
Zad. 3. Peano w języku polskim odmienia się (jak większość nazwisk obcojęzycznych), zatem wersja nieodmieniona - krzywa Peano - jest niepoprawna. Jest to nazwisko włoskie i nie może być odmieniane zgodnie z regułami odmiany nazwisk polskich, zatem wersja krzywa Peany jest niepoprawna. Zgodnie z regułami odmiany nazwisk włoskich w języku polskim poprawną wersją dopełniacza jest krzywa Peana (podobnie jak wzory Cardana, nie Cardano, ani Cardany). Więcej o odmianie nazwisk matematyków piszemy na Portalu tutaj.
Regułę odmiany włoskich nazwisk w języku polskim podaje np. "Słownik Języka Polskiego" PWN.
Wyszukiwarka Google (po wpisaniu wyrażeń w cudzysłowie) podaje stosunek wystąpień haseł krzywa Peano : krzywa Peana : krzywa Peany zbliżony do stosunku liczb 1 : 3,6 : 0,03. Jak widać wersja poprawna wcale nie jest najbardziej popularna.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
