Zad. 1. Ile jest pierwszych liczb dwucyfrowych, których nie można uzyskać jako sumy dwóch liczb palindromicznych (tzn. takich, które nie zmieniają się czytane wprzód i wspak)?
Zad. 2. Jacek, Wacek, Placek i Pankracek chcą kupić grę komputerową. Jackowi brakuje 137 zł, Wackowi 136 zł, Plackowi 4 zł, a Pankrackowi 135 zł. Postanowili, że kupią tę grę wspólnie, a potem będą się nią wymieniali. Okazało się jednak, że nadal brakuje im pieniędzy. Ile kosztowała gra, jeśli jej cena wyrażała się pełną liczbą złotych?
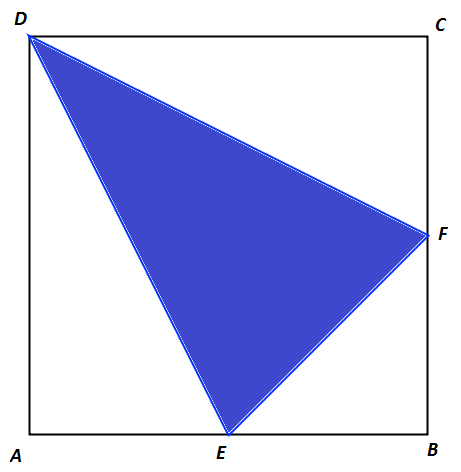
Zad. 3. W kwadracie o obwodzie 8 cm środki dwóch sąsiednich boków połączono ze sobą nawzajem i z wierzchołkiem kwadratu nienależącym do tych boków. Jaką część pola kwadratu stanowi pole otrzymanego na środku trójkąta?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Konrad Andruchów - SP 4 Bolesławiec, Jakub Badowski - SP Mszczonów, Gracjan Ciupa - SP 72 Wrocław, Maja Frankowska - SP 3 Lubin, Norbert Frydrysiak - SP Mszczonów, Joachim
Górski - SP Mszczonów, Antoni Kołat - SP 45 Wrocław, Marek Komorowski - SP 5 Żory, Natalia
Krystkiewicz - KSP Mława, Martyna Kubiak - SP Skoki, Szymon Kubiak - SP Skoki, Janina Popławska - SP 4 Legnica, Jakub Ptak - SP 64 Wrocław, Natasza Ptak - SP 118 Wrocław, Kaja Srokosz - SP 52 Warszawa, Bartosz Szczerba - SP 35 Szczecin, Wiktor Szywała - SP 1
Sobótka, Michał Świerkowski - SP 215 Warszawa, Jerzy Wąsiewicz - SP Kostowiec, Michalina Więckowska - SP 1 Konstancin-Jeziorna i Aleksandra Zalewska - SP 1 Sokółka; - 2 pkt. - Łukasz Banaś - SP 46 Wrocław, Mieszko Baszczak - SP 301 Warszawa, Mikołaj Bilski - SP 6 Jelenia Góra, Antoni Bryszewski - SP 15 Jelenia Góra, Lena Bukowska - SP 1 Sobótka, Antoni Buraczewski - SP 107 Wrocław, Hubert Cabaj - SP Brzoza, Hubert Cymbalista - SP 1 Sobótka, Michał Gębarowski - SP Polna, Malwina Górecka - SP 11 Inowrocław, Szymon Grech - NSP Koszarawa Bystra, Hubert Grześkowiak - SP Mieroszów, Natasza Henko - SP Mieroszów, Igor Hołowacz - SP Bielany Wrocławskie, Zuzanna Jóźków - SP 1 Sobótka, Gabriela Kelner - SP Mieroszów, Michalina Kulesza - SP Brzoza, Kacper Kuszaj - SP 2 Jelcz-Laskowice, Zuzanna Prasek - SP Mieroszów, Karol Raczkowski-Orleski - SP 45 Wrocław, Mikołaj Roszczyk - SP 7 Legionowo, Adam Stachelek - SP 301 Warszawa, Klaudia Sułkowska - SP Mieroszów, Szymon Warmuła - SP Kobierzyce i Kacper Żywień - SP 113 Wrocław;
- 1 pkt. - Mikołaj Cholewiński - SSP 35 Legionowo, Katarzyna Czarna PSP 1 Brzeg, Mateusz Krakowiak - SP 74 Wrocław i Adam Szyszka - SP 3 Gogolin.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po pięciu miesiącach Ligi Zadaniowej dla SP prowadzą: Gratulujemy!
Zad. 1. Jest tylko jedna taka liczba, mianowicie 43. Liczby pierwsze dwucyfrowe to: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 i 97. Liczby palindromiczne mniejsze od 100 są jednocyfrowe lub dwucyfrowe o jednakowych cyfrach. Sumując dwie takie liczby nie osiągniemy nigdy wyników dwucyfrowych równych: 21, 32, 43, 54, 65, 76, 87 i 98. Wśród nich tylko 43 jest liczbą pierwszą.
Zad. 2. Jeśli przez x oznaczymy szukaną cenę gry komputerowej, to kwoty pieniędzy, jakimi dysponują chłopcy, są równe x-137, x-136, x-4 i x-135. Razem mają 4x-412 zł i jest to kwota mniejsza niż x. Stąd cena gry musi być mniejsza niż 412/3 = 137 i 1/3, a ponieważ cena ta była wyrażona w pełnych złotych, wynosi 137 zł. Mniej nie może, bo w takim wypadku Jackowi brakowałaby do tej ceny ujemna ilość pieniędzy.
Zad. 3. Bok kwadratu ABCD ma długość 8/4 = 2 cm. Stąd pole trójkąta EBF wynosi 0,5 cm2, a suma pól trójkątów AED i FCD jest połowę pola kwadratu ABCD, czyli wynosi 2 cm2. Stąd można obliczyć, że pole trójkąta EFD stanowi 3/8 pola kwadratu ABCD.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
