Zad. 1. Liczba 5655 podzielona przez tajemniczą naturalną liczbę dwucyfrową daje resztę 11, a liczba 5879 podzielona przez tę samą tajemniczą liczbę daje resztę 14. Ile wynosi suma cyfr tajemniczej liczby?
Zad. 2. Liczby całkowite dodatnie m i n spełniają warunek 10·2m = 2n + 2n+2. Jaka jest dodatnia różnica między nimi?
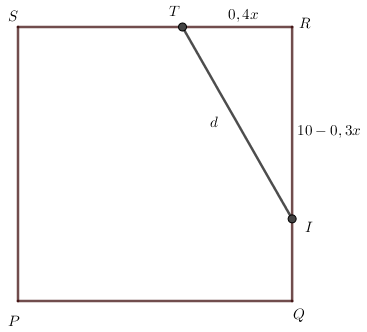
Zad. 3. W różanym ogrodzie w kształcie kwadratu PQRS o boku 10 m biedronka Ilonka wyruszyła z wierzchołka Q i maszerowała wzdłuż krawędzi QR w tempie 30 cm/min. W tej samej chwili pajęczyca Tekla wyruszyła z wierzchołka R wzdłuż krawędzi RS w tempie 40 cm/min. Jaka będzie najkrótsza dzieląca je odległość?
W listopadzie punkty zdobyli:
- 3 pkt. – Zuzanna Basińska SP 11 Inowrocław, Olga Bazelska SP 11 Inowrocław, Patryk Boruń SP 9 Wałbrzych, Artur Bumażnik SP 1 Piechowice, Emilia Cichowska SP 14 Lubin, Paweł Czarny SP 36 Wrocław, , Kacper Kazik SP 4 Inowrocław, Weronika Kiniorska SP 65 Wrocław, Filip Klich SP Ekola Wrocław, Klara Kogut SP 9 Gliwice, Szymon Kuźniar SP Ciechów, Paweł Lisztwan SP 3 Mikołów, Julia Marcinkowska 1 Białystok, 11 Inowrocław, Paweł Michałowski, PSP Weronika Michałowska PSP 1 Białystok, Tymosz Srokosz SP 52 Warszawa, Nadia Stefanowska SP 10 Legnica, Karol Szaniewski SP 16 Studzienice, Alicja Szwarczyńska SP Kowalowa, Weronika Tracz SP Stare Bogaczowice, Oksana Zatwardnicka SP 28 Wałbrzych;
- 2 pkt. – Aleksandra Antonowicz SP 28 Wałbrzych, Ewa Bogacz SP 76 Wrocław, Natalia Cubala SP Jedlnia-Letnisko, Łukasz Ganczarek SP 10 Wrocław, Amelia Gugała SP Wrzosów, Paulina Hołodniuk SP 2 Wołów, Sandra Łuczak SP 107 Wrocław, Maja Jas SP 5 Strzelin, Miłosz Kiełbasa SP 2 Tomaszów Lubelski, Jan Krupa SP2 Tomaszów Lubelski, Piotr Laszkiewicz SP 11 Jelenia Góra, Zuzanna Lipka SP Jedlnia–Letnisko, Maya Małachowska SP 3 Głogów, Jullita Masłowska SP 3 Głogów, Natalia Mucha SP 28 Wałbrzych, Maja Muszyńska SP Jedlnia-Letnisko, Olaf Pawka SP Józefów n. Wisłą, Agnieszka Płudowska SP18 Lublin, Filip Timofiejczuk SP 3 Tarnowskie Góry, Franciszek Zakrawacz SP 9 Wałbrzych, Miłosz Zakrzewski SP Gostycyn;
- 1 pkt. – Tristan Bronowicki SP Żórawina, Zuzanna Dropia SP Świerże Górne, Martyna Gruszczyńska SP 19 Gliwice, Hanna Kubiak SP Żórawina, Natalia Olasz SP Żórawina, Dominika Zadworna SP 4 Grodzisk Wlkp,.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x oznacza szukaną liczbę dwucyfrową i niech 5655:x = k r.11 oraz 5879:x = l r.14. Otrzymujemy układ równań xk+11 = 5655, xl+14 = 5879, z którego po przekształceniach mamy x(l–k) = 221, czyli x(l–k) = 13.17. Liczba 17 spełnia warunki zadania, a suma jej cyfr wynosi 8.
Zad. 2. Przekształcając równość 10·2m = 2n+2n+2, wyliczamy, że szukana różnica wynosi 1.
2m+1·5 = 2n + 4·2n
2m+1·5 = 5·2n
2m+1 = 2n
m+1 = n
n–m = 1
Zad. 3. Niech x oznacza czas ruchu biedronki (i pajęczycy) od chwili startu. Drogi pokonane w tym czasie przez każdą z nich wynoszą odpowiednio 04x i 10–0,3x. Niech d oznacza odległość między nimi po upływie czasu x. Z twierdzenia Pitagorasa mamy d2 = (0,4x)2 + (10–0,3x)2, czyli d2 = 0,25x2–6x+100. Z wykresu odczytujemy, że po 12 minutach kwadrat odległości (czyli także sama odległość d) osiąga wartość najmniejszą: można łatwo sprawdzić, że dla x=0 oraz x=24 otrzymamy d2=100, a z symetrii wykresu wiemy, że najmniejsza wartość wypadnie na jego osi symetrii, czyli na środku pomiędzy 0 i 24). Obliczamy, że dla x=12 mamy d2 = 0,25·144–6·12+100 = 64, skąd d=8 metrów.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
