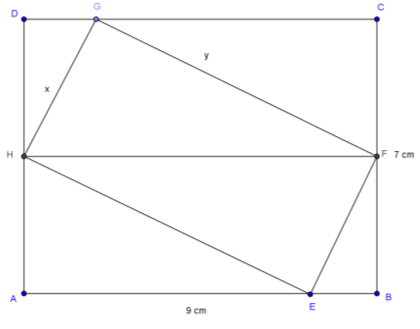
Zad. 1. W prostokącie o wymiarach 9 cm na 7 cm umieszczono mniejszy prostokąt tak, że jedna z jego przekątnych łączy środki krótszych boków większego prostokąta, a dwa pozostałe wierzchołki małego leżą na dłuższych bokach dużego prostokąta. Jaki obwód ma mniejszy z prostokątów?
Zad. 2. Znajdź wszystkie pary liczb naturalnych spełniających równanie x2 – 102 = y2 + 102.
Zad. 3. Rowerzysta jechał ze stałą prędkością z Pieskowej Skały do Kotkowego Głazu. Po dwóch godzinach jazdy pozostało mu do przejechania jeszcze 5 km. O ile szybciej musiałby jechać, aby całą trasę pokonać w dwie godziny?
W kwietniu punkty zdobyli:
- 3 – Artur Bumażnik SP 1 Piechowice, Mateusz Galik SP Arka Wrocław, Aleksander Kiszkowiak SP 66 Warszawa, Mateusz Koba SP 3 Cieszyn, Michał Licznarowski SP 66 Warszawa, Dominika Miturska SP 66 Warszawa, Joanna Nowakowska SP 3 Głogów, Wiktoria Pietrzak SP 3 Głogów, Arkadiusz Piwowarczyk SP 14 Ostrowiec Świętokrzyski, Bartosz Podlak SP 3 Cieszyn, Oliwia Stańczyk SP Aslan Głogów, Dominika Wojdacz SP 11 Inowrocław;
- 2,5 – Faustyna Doliwka SP Łobżenica;
- 2 – Monika Budzeń SP 7 Leszno, Kacper Kozak SP Tyniec Mały, Paweł Lisztwan SP 3 Mikołów, Marta Pieczonka SP 3 Cieszyn, Oliwia Raszewska SP 6 Boguszów-Gorce, Igor Sudyka SP 2 Jasło, Alicja Szwarczyńska SP Kowalowa, Kacper Wereszczyński SP 3 Mikołów, Anastasia Yakovleva SP 3 Mogilno;
- 1,5 – Miłosz Zakrzewski SP Gostycyn, Amelia Żuczek SP 2 Wieliczka;
- 1 – Aniela Przystał SP Ciechów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Trójkąt HFG jest prostokątny. Jego pole możemy zapisać na dwa sposoby: PHFG = 1/2.xy i PHFG = 1/2.9.2,5. Wówczas 1/2.xy = 15,75, czyli 2xy = 63. Z twierdzenia Pitagorasa otrzymujemy x2+y2 = 81. Dodając stronami ostatnie dwa równania otrzymujemy 2xy+x2+y2 = 63+81, czyli (x+y)2 = 144, a stąd x+y=12. Obwód mniejszego prostokąta wynosi zatem 2(x+y) = 24 cm.
Zad. 2. Skoro x2–102 = y2+102, to (x–y)(x+y) = 200. Ponieważ 200 = 1.200 = 2.100 = 4.50 = 5.40 = 8.25 = 10.20, rozwiązań zadania należy szukać wśród rozwiązań układów równań:
[tex]\left\{\begin{array}{rcl}x-y&=&1\\x+y&=&200\end{array}\right.[/tex], [tex]\left\{\begin{array}{rcl}x-y&=&2\\x+y&=&100\end{array}\right.[/tex], [tex]\left\{\begin{array}{rcl}x-y&=&4\\x+y&=&50\end{array}\right.[/tex], [tex]\left\{\begin{array}{rcl}x-y&=&5\\x+y&=&40\end{array}\right.[/tex], [tex]\left\{\begin{array}{rcl}x-y&=&8\\x+y&=&25\end{array}\right.[/tex], [tex]\left\{\begin{array}{rcl}x-y&=&10\\x+y&=&20\end{array}\right.[/tex].
Wśród rozwiązań tych układów znajdujemy trzy pary liczb naturalnych stanowiących rozwiązanie zadania: 51 i 49, 27 i 23, 15 i 5.
Zad. 3. Oznaczmy przez v – prędkość rowerzysty, a przez x - szukany przyrost prędkości. Z treści zadania wynika, że 2v+5 = 2(v+x), skad x = 2,5. Rowerzysta powinien jechać o 2,5 km/h szybciej.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
