Zad. 1. Udowodnij, że dla x>0, zachodzi [tex]x+\frac{4}{x^2}\geq 3[/tex].
Zad. 2. W prostokątnym układzie współrzędnych zaznacz obszar złożony z par liczb (x, y) spełniających poniższy układ nierówności. Oblicz jego pole.
[tex]\left\{\begin{array}{rcl}|y-x|&\leq&1\\|x+3|&\leq&1\end{array}\right.[/tex]
Zad. 3. Dwa okręgi styczne zewnętrznie są styczne wewnętrznie do trzeciego okręgu o promieniu 5 cm. W jakim przedziale znajduje się pole trójkąta wyznaczonego przez środki tych okręgów? Odpowiedź uzasadnij.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kacper Gembara G w ZSS Wołów, Konrad Litwiński G 86 Warszawa i Przemysław Rybarczyk G Integracyjne Stargard Szczeciński;
- 2,5 pkt. - Zofia Ogonek G 58 Warszawa i Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski;
- 2 pkt. - Oliwia Kropidłowska G 1 Wrocław i Mateusz Rzepecki G 14 Wrocław;
- 1,5 pkt. - Helena John G Wielowieś i Joanna Lisiowska KZE Warszawa;
- 1 pkt. - Aleksandra Domagała G 23 Wrocław i Magdalena Owczarek G Dwujęzyczne Legionowo;
- 0,5 pkt. - Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po siedmiu miesiącach Ligi Zadaniowej z wynikiem 21 pkt. (na 21 możliwych) prowadzi: Konrad Litwiński. Drugie miejsce z wynikiem 20,5 pkt. zajmują: Michał Stempniak. Trzecie miejsce z wynikiem 20 pkt. zajmuje: Mateusz Rzepecki. Gratulujemy!
Zad. 1. Ponieważ x>0, pomnóżmy obie strony nierówności przez x2.
[tex]x+\frac{4}{x^2}\geq 3[/tex]
[tex]x^3-3x^2+4\geq 0[/tex]
[tex]x^3+x^2+4-4x^2\geq 0[/tex]
[tex]x^2(x+1)+4(1-x)(1+x)\geq 0[/tex]
[tex](x+1)(x^2-4x+4)\geq 0[/tex]
[tex](x+1)(x-2)^2\geq 0[/tex]
Z założenia x>0, mamy więc (x+1)>1 oraz zawsze zachodzi (x-2)2>0, co kończy dowód.
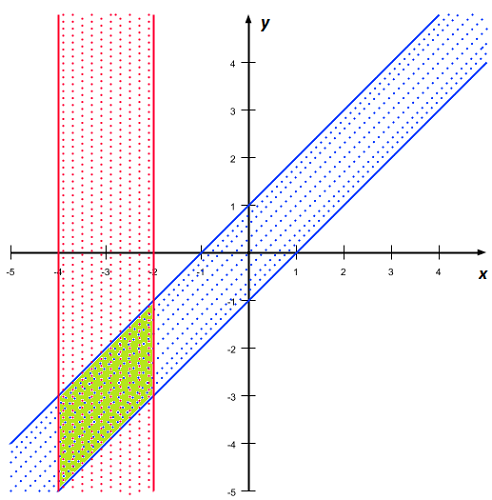
Zad. 2. Rozwiązaniem jest figura wyznaczona przez przecięcie nieograniczonego pasa -4≤x≤-2 (obszar czerwony) z pasem położonym pomiędzy prostymi równoległymi y=x-1 i y=x+1 (obszar niebieski). Jest to równoległobok o podstawie i wysokości 2, więc jego pole wynosi 4.
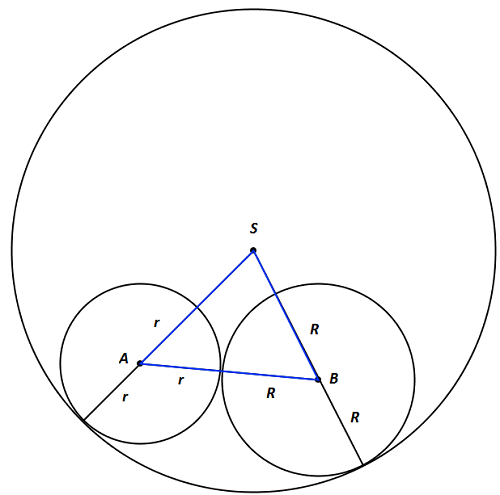
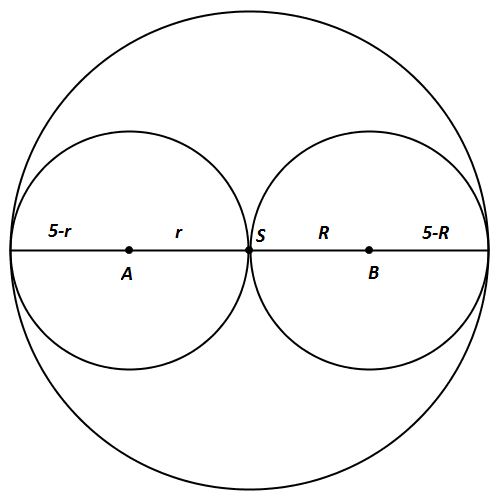
Zad. 3. Obwód trójkąta ABS wynosi 10 cm (patrz zadanie 3 dla SP). Przy ustalonym obwodzie trójkąt ma największe pole, gdy jest równoboczny (rysunek 1) - patrz dowód poniżej. Wtedy jego pole wynosi 25/9√3 cm2. Najmniejsze pole otrzymamy w przypadku trójkąta zdegenerowanego, gdy środki obu mniejszych okręgów leżą na średnicy większego okręgu (rysunek 2). Wynosi ono 0 cm2. Stąd pole trójkąta ABS zawiera się w przedziale [0, 25/9√3].
Twierdzenia izoperymetryczne dotyczą figur o stałym obwodzie. Nazwa pochodzi od greckich słów isos = stały i perimetr = obwód.
Twierdzenie izoperymetryczne dla trójkątów
Ze wszystkich trójkątów o ustalonym obwodzie największe pole ma trójkąt równoboczny.
Uzasadnienie
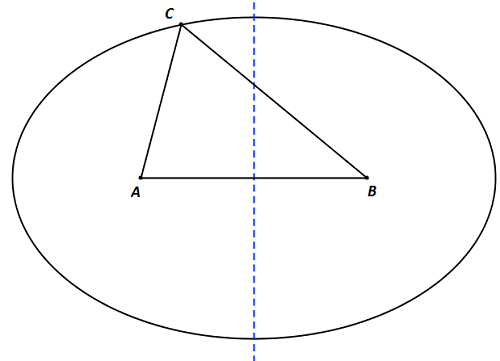
Załóżmy nie wprost, że trójkąt ABC o danym obwodzie i maksymalnym polu nie jest równoboczny. Wobec tego ma dwa boki o różnych długościach. Załóżmy, że wychodzą one z wierzchołka C. Wierzchołek ten leży na pewnej elipsie o ogniskach w punktach A i B, a poruszając punktem C po tej elipsie, nie zmieniamy obwodu trójkąta ABC, bo elipsa z definicji jest zbiorem punktów o jednakowej sumie odległości od ognisk. Ponieważ odległości AC i BC były różne, punkt C nie leżał na symetralnej odcinka AB. Zatem przesuwając go wzdłuż elipsy do jej najwyższego punktu nad prostą AB, zwiększamy wysokość trójkąta opuszczoną na AB, a zatem zwiększamy jego pole, wbrew założeniu. Otrzymujemy sprzeczność, co dowodzi prawdziwości wyjściowego twierdzenia.
Uogólnienie 1 (twierdzenie izoperymetryczne dla n-kątów, tzw. twierdzenie Zenodora)
Ze wszystkich n-kątów o ustalonym obwodzie największe pole ma n-kąt foremny.
Uogólnienie 2 (twierdzenie izoperymetryczne, tzw. twierdzenie Dydony)
Ze wszystkich figur o ustalonym obwodzie największe pole ma koło.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
