Zad. 1. Rozwiąż równanie:$$\frac{1}{1+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+\ldots+\frac{1}{\sqrt{2x+1}+\sqrt{2x+3}}=16 \ .$$
Zad. 2. Do 10% roztworu soli kuchennej dosypano 60 dag soli, otrzymując roztwór o stężeniu mniejszym niż 16%. Ile w tym roztworze mogło być soli, a ile wody?
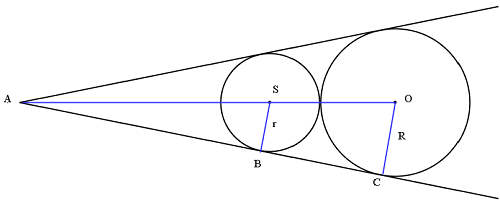
Zad. 3. Dwa koła styczne zewnętrznie są jednocześnie styczne do ramion pewnego kąta. Jaka jest różnica pól tych kół, jeśli odległości ich środków od wierzchołka kąta wynoszą 50 cm i 30 cm?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Konrad Litwiński G 86 Warszawa, Mateusz Rzepecki G 14 Wrocław i Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski,
- 2,5 pkt. - Kacper Gembara G w ZSS Wołów, Joanna Lisiowska KZE Warszawa i Krzysztof Żmuda G Wieczfnia Kościelna,
- 2 pkt. - Aleksandra Domagała G 23 Wrocław, Oliwia Kropidłowska G 1 Wrocław, Zofia Ogonek G 58 Warszawa, Marcin Oleksy G Lewin Brzeski i Przemysław Rybarczyk G Integracyjne Stargard Szczeciński,
- 1,5 pkt. - Helena John G Wielowieś, Iwo Pilecki-Silva G 26 Wrocław i Olga Sławatyniec G 2 Kamienna Góra,
- 1 pkt. - Izabela Czaja G Nagawczyn i Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie,
- 0,5 pkt. - Magdalena Owczarek G Dwujęzyczne Legionowo.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Po trzech miesiącach Ligi Zadaniowej z wynikiem 9 pkt. (na 9 możliwych) prowadzą: Konrad Litwiński, Mateusz Rzepecki i Michał Stempniak. Drugie miejsce z wynikiem 8 pkt. zajmują: Kacper Gembara, Oliwia Kropidłowska i Zofia Ogonek. Trzecie miejsce z wynikiem 7,5 pkt. zajmują: Joanna Lisiowska, Iwo Pilecki-Silva i Krzysztof Żmuda. Gratulujemy!
Zad. 1. Równanie spełnia liczba 543. Usuwając niewymierności z mianowników, dostaniemy:$$\frac{1-\sqrt{3}}{-2}+\frac{\sqrt{3}-\sqrt{5}}{-2}+\ldots+\frac{\sqrt{2x+1}-\sqrt{2x+3}}{-2}=16,$$co po uproszeniu daje [tex]-\frac{1}{2}+\frac{\sqrt{2x+3}}{2}=16.[/tex]
To równanie sprowadzamy do postaci √(2x+3) = 33. Obie strony są dodatnie, więc podnosimy je do kwadratu (bez wprowadzania pierwiastków obcych) i po dalszych uproszczeniach otrzymujemy równanie x=543, które jest równoważne z wyjściowym.
Zad. 2. W roztworze mogło być przynajmniej 840 g soli i przynajmniej 7,56 l wody, przy czym wody musiało być (wagowo) dziewięć razy więcej niż soli. Oznaczmy przez w masę wody, a przez s masę soli w roztworze 10-procentowym. Mamy wówczas s/w+s=0,1, co po przekształceniach daje w=9s. Po dodaniu 60 dag soli sytuację w roztworze opisuje nierówność (s+600)/(w+s+600) ≤ 0,16, która po przekształceniach daje 840 ≤ s. Stąd 7560 ≤ w.
Zad. 3. Różnica pól kół wynosi 100π. Niech r i R oznaczają promienie odpowiednio mniejszego i większego koła. Ponieważ trójkąty prostokątne ABS i ACO są podobne, zachodzi proporcja r/|AS| = R/|AO|, czyli r/30 = R/50. Ponadto zachodzi warunek styczności kół |SO| = r+R = 50-30 = 20. Rozwiązując układ tych dwóch równań, otrzymamy r = 7,5 cm oraz R = 12,5 cm. Stąd różnica pól obu kół to π(R2-r2) = 100π.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
