W listopadzie 2014 ze względu na wybory do samorządów lokalnych często publikowano w mediach sondaże poparcia dla partii politycznych lub dla poszczególnych kandydatów. Najczęściej graficzną ilustrację wyników tych sondaży stanowiły wykresy słupkowe. Pewien szczególny rodzaj wykresu słupkowego występujący w statystyce nazywamy histogramem, ale trzeba pamiętać, że nie jest nim każdy wykres słupkowy.
Przykład. W ligowym zadaniu z października pojawiły się dane dotyczące liczby rodzeństwa uczniów pewnej klasy. Powiedziano tam, że troje z nich było jedynakami, dziesięcioro miało jednego brata lub siostrę, ośmioro miało dwoje rodzeństwa, troje trójkę i jedno czwórkę. Informacje te można przedstawić w tabelce:
| liczba rodzeństwa | liczba uczniów |
| 0 | 3 |
| 1 | 10 |
| 2 | 8 |
| 3 | 3 |
| 4 | 1 |
Na te dane możemy spojrzeć nieco inaczej, zastępując konkretne liczby rodzeństwa przedziałami, np. tak, jak pokazano poniżej.
| liczba rodzeństwa w przedziale | liczba uczniów |
| [0, 1) | 3 |
| [1, 2) | 10 |
| [2, 3) | 8 |
| [3, 4) | 3 |
| [4, 5) | 1 |
Poza podanym w tabelce przedziałami nie ma już żadnej obserwacji.
Liczby rodzeństwa należą oczywiście do zbioru niedużych liczb naturalnych, więc podział na przedziały nie jest w tym przypadku szczególnie przydatny. Gdybyśmy jednak mówili np. o wzroście uczniów, pogrupowanie obserwacji w przedziały o długości np. 10 cm byłoby już bardzo naturalne.
Na podstawie tabelki możemy łatwo stworzyć wykres słupkowy, w którym liczbę rodzeństwa będzie reprezentował słupek o odpowiedniej wysokości (patrz niżej).
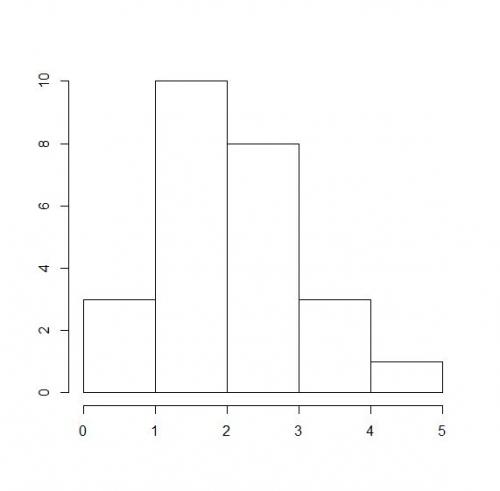
Wykres, na którym w postaci słupków umieszczonych nad odpowiednimi przedziałami zilustrowano liczby obserwacji, jakie znalazły się w poszczególnych przedziałach, nazywamy właśnie histogramem.
Dobór przedziałów
To czy przedziały, w jakich zliczamy obserwacje, są lewo- czy prawostronnie domknięte, jest kwestią umowną i nie ma większego znaczenia. Umawiamy się zatem, że będziemy wybierali przedziały lewostronnie domknięte (a prawostronnie otwarte).
Istotną kwestią jest natomiast wybór przedziałów użytych do sporządzenia histogramu. Na ogół wybiera się przedziały równej długości, ponieważ dają one oglądającemu diagram stosunkowo najlepsze i najbardziej naturalne rozeznanie w strukturze danych (ze względu na to, jak odbieramy i interpretujemy wrażenia wizualne).
A jaka powinna być długość przedziałów? Jak powinny one być położone na osi? To wszystko zależy od tego, z jakimi danymi mamy do czynienia, ale dokonanie właściwego wyboru jest niezwykle istotne dla wygodnej analizy diagramu. Jeśli dane składają się z kilku bliskich liczb naturalnych (jak w przykładzie z rodzeństwem), typowy wybór pada na przedziały zawierające po jednej liczbie naturalnej. Jednak gdy możliwych wartości jest dużo, albo są znacznie rozrzucone na osi, albo nie są to liczby naturalne, zasadnym jest wyznaczenie przedziałów o większej długości (obejmujących więcej liczb naturalnych).
Gdybyśmy badali wzrost uczniów mierząc ich linijką z podziałką milimetrową, a wyniki wyrażali w centymetrach, wówczas jako obserwacje możemy otrzymać wartości niekoniecznie naturalne, choć niektóre mogą być bardzo zbliżone, nawet jeśli żadne nie będą jednakowe. Wówczas wyznaczenie niewielkich przedziałów (np. 1-, 5- lub 10-centymetrowych), w obrębie których będziemy zliczać obserwacje, wydaje się bardziej naturalne. To jak długie powinny być przedziały, zależy od wiekości rozrzutu obserwacji. Jeśli wybierzemy przedziały zbyt krótkie, może się okazać, że wiele z nich nie będzie zawierało żadnej obserwacji i na sporządzonym w ten sposób histogramie nie zauważymy żadnej prawidłowości w rozkładzie danych. Z kolei jeśli przedziały będą zbyt długie, grupując w nich dane, utracimy wiele cennych informacji. Można więc powiedzieć, że rysowanie histogramów (a właściwie wyznaczanie przedziałów, w obrębie których będą zliczane obserwacje) jest zadaniem, które wymaga pewnego kunsztu i doświadczenia.
Rodzaje histogramów
Wśród rozmaitych sposobów, w jakie mogą układać się słupki histogramu, możemy wyróżnić trzy szczególne układy:
- dane symetryczne (jak niżej)
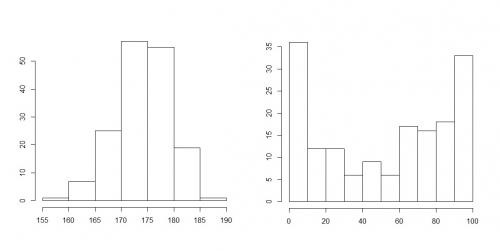
- dane lewostronnie asymetryczne (jak niżej)
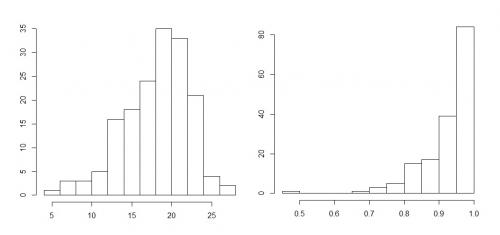
- dane prawostronnie asymetryczne (jak niżej)
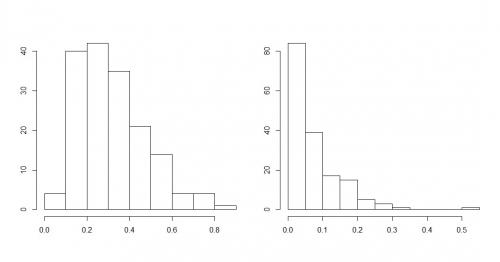
Obrazowo można powiedzieć, że dane są symetryczne, jeśli jest mniej więcej tyle samo małych obserwacji co dużych. Z kolei dane są lewostronnie asymetryczne, jeśli w zbiorze danych jest mało małych obserwacji i dużo dużych, natomiast dane są prawostronnie asymetryczne, jeśli jest dużo małych obserwacji a mało dużych.
Histogram to bardzo użytecznie narzędzie do badania symetrii danych. Czasem jednak potrzebujemy liczbowego opisu tej symetrii. Gdybyśmy nieco dokładnej zbadali sytuacje przedstawione na powyższych diagramach (analizując szczegółowo dane, na podstawie których wykresy zostały sporządzone), przekonalibyśmy się, że typ diagramu zależy od relacji między średnią a medianą zestawu danych:
- gdy dane są symetryczne, wówczas średnia jest bliska medianie,
- gdy dane są lewostronnie symetryczne, wówczas średnia jest znacząco mniejsza od mediany,
- gdy dane są prawostronnie symetryczne, wówczas średnia jest znacząco większa od mediany.
Miary symetrii danych
Wobec tego wydaje się, że stopień asymetrii danych moglibyśmy mierzyć różnicą średniej próbkowej i mediany. Trzeba jednak tę wielkość "wyskalowwać" w taki sposób, aby ocena symetrii nie zależała od wielkości danych (czy są to liczby małe, czy duże), ale od ich rozrzutu. Aby uzyskać ten efekt, różnicę średniej i mediany zestawu danych trzeba podzielić przez odchylenie standardowe. W ten sposób otrzymujemy tzw. współczynnik skośności danych. Jeśli zbiór danych składa się z liczb x1, x2,..., xn, to współczynnik skośności wyraża się jako:
[tex]A(x_1,x_2,\dots,x_n)=\frac{\overline{x}-m(x_1,x_2,\dots,x_n)}{s(x_1,x_2,\dots,x_n)},[/tex] gdzie m(x1, x2, ..., xn) oznacza medianę liczb x1, x2,..., xn.
Można zatem powiedzieć, że dla danych symetrycznych współczynnik skośności jest bliski zera, dla danych lewostronnie asymetrycznych współczynnik skośności jest istotnie ujemny, zaś dla danych prawostronnie asymetrycznych współczynnik skośności jest istotnie dodatni. Pojawiające się tu określenia "bliski zera", "istotnie ujemny" i "istotnie dodatni" mogą razić osoby, które są przyzwyczajone do ścisłych matematycznych sformułowań. Jednak gdy mamy do czynienia z danymi, czasem istotna jest ich ocena jakościowa, a nie wyznaczanie precyzyjnych granic między poszczególnymi przypadkami. Zatem to, czy jakieś dane zostaną uznane za asymetryczne lub symetryczne (a może jako nienależące do żadnej z tych kategorii), zależy w dużej mierze od subiektywnego wrażenia osoby, która dokonuje takiej analizy. Dlatego lepiej jest kwalifikować dane do jednej z tych kategorii wizualnie (tzn. opierając się na histogramie) niż na współczynniku asymetrii. Ten przyda się raczej wtedy, gdy już zakwalifikujemy dane "na oko" do jednej z grup i będziemy chcieli porównać stopień asymetrii kilku zbiorów danych w obrębie jednej kategorii (tzn. sprawdzić, który z nich jest bardziej asymetryczny).
Nie należy zapominać, że oprócz symetrii oraz lewo- i prawostronnej asymetrii można jeszcze wyróżnić zbiory danych, które nie należą do żadnej z tych kategorii, jednak do wykrywania takich przypadków współczynnik skośności danych nie jest użyteczny.
Zad. 1. Na podstawie histogramów oceń symetrię następujących zbiorów danych:
a) 7,9; 8,7; 3,7; 6,7; 7,1; 1,7; 11,3; 13,3; 6,3; 12,1; 8,3; 9,2; 4,2; 10,8; 2,9; 9,7; 4,7; 5,3; 5,8; 10,3;
b) 24; 26; 30; 10; 17; 20; 50; 77; 87; 103; 55; 61; 66; 71; 129; 34; 37; 39; 46; 42.
Sam dobierz przedziały, jakimi się posłużysz do sporządzenia histogramów. Nie musisz wysyłać rysunków. Wystarczy, że napiszesz, jakie przedziały wyróżniłeś i ile znalazło się w nich obserwacji.
Zad. 2. Dla powyższych danych oblicz ich współczynniki skośności. Porównaj informacje uzyskane za ich pomocą z tymi, które uzyskałeś w poprzednim zadaniu.
Zad. 3. Załóżmy, że mamy dwie obserwacje a i b. (Zbiór danych złożony z dwóch obserwacji z pewnością możemy uznać za symetryczny). Następnie wylosowaliśmy trzecią obserwację x, o której wiemy, że należy do przedziału [a, b]. Jakie powinno być x, abyśmy mogli powiedzieć, że symetria danych została zaburzona najbardziej jak to możliwe przez dodanie x? Uzasadnij odpowiedź.
Zad. 1. Do każdej obserwacji ze zbioru x1, x2, ..., xn dodano tę samą liczbę a. Jak zmieni to współczynnik skośności danych?
Zad. 2. Każdą obserwację ze zbioru x1, x2, ..., xn pomnożono przez tę samą różną od zera liczbę b. Jak zmieni to współczynnik skośności danych?
Zad. 3. Dysponujemy zbiorem danych 1, 2, ..., n dla pewnego naturalnego n≥3. Taki zbiór danych jest niewątpliwie symetryczny. Okazuje się jednak, że symetrię tę - gdyby mierzyć ją tylko współczynnikiem skośności - możemy dowolnie mocno zaburzyć poprzez dodanie tylko jednej obserwacji. Do zbioru dokładamy jeszcze jedną obserwację x, o której wiemy, że jest większa od wszystkich poprzednich. Jaki warunek musi spełniać x, aby współczynnik skośności był większy od pewnej ustalonej liczby naturalnej c>0?
W rozwiązaniu mogą okazać się przydatne następujące tożsamości, które możecie znać ze szkoły:
[tex]1+2+...+n=\frac{n(n+1)}{2}[/tex]
[tex]1^2+2^2+...+n^2=\frac{n(n+1)(2n+1)}{6}[/tex]
W grudniowym etapie Ligi z Analizy danych przyznano punkty w sposób następujący:
- Aleksandra Domagała z G 23 we Wrocławiu i Joanna Lisiowska z Katolickiego G w Warszawie - 3 punkty,
- Mieszko Baszczak z SP 301 w Warszawie - 2,5 punktu,
- Kacper Toczek z G 2 w Wołowie - 1 punkt,
- Kaja Grabowska z G 2 w Wołowie - 0,5 punktu.
Na prowadzeniu wciąż Aleksandra Domagała (I miejsce). Kolejne lokaty zajmują: Joanna Lisiowska (II miejsce) i Mieszko Baszczak (III miejsce).
W grudniowym etapie Ligi z Analizy danych swój dorobek punktowy powiększyli:
- Tomasz Stempniak z I LO w Ostrowie Wielkopolskim - o 3 punkty,
- Daria Bumażnik z II LO w Jeleniej Górze - o 1,5 punktu.
W ten sposób klasyfikacja nie uległa zmianie i wciąż prowadzi Tomasz Stępniak (I miejsce)
przed Darią Bumażnik (II miejsce) i Krzysztofem Danielakiem (III
miejsce).
Zad. 1.
Przykładowe histogramy sporządzone na podstawie podanych zestawów danych znajdują się na rysunku poniżej (po lewej dane z punktu a), po prawej z punktu b)). Dla danych z punktu a) wybrano następujące przedziały: [0,2); [2,4); [4,6); [6,8); [8,10); [10,12); [12,14). Dla danych z punktu b) wybrano następujące przedziały: [0,20); [20,40); [40,60); [60,80); [80,100); [100,120); [120,140). Liczby obserwacji w poszczególnych przedziałach można łatwo odczytać z rysunków.
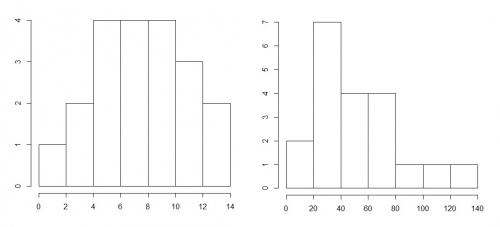
Tak sporządzone histogramy pozwalają wnioskować, że dane z punktu a) są symetryczne, zaś dane z punktu b) są prawostronnie asymetryczne.
Zad. 2.
a) [tex]\frac{7,5-7,5}{\sqrt{9,794}}=0[/tex]
Na podstawie histogramu oceniamy, że dane są symetryczne. Obliczony współczynnik skośności nie przeczy temu.
b) [tex]\frac{51,2-44}{\sqrt{891,46}}\approx 0,241[/tex]
Na podstawie histogramu oceniamy, że dane są prawostronnie asymetryczne. Obliczony współczynnik skośności jest dodatni, a więc nie przeczy temu.
Zad. 3. Symetria danych będzie najbardziej zaburzona, jeśli x=a lub x=b. Łatwo można to zobaczyć, sporządzając dowolny histogram oparty na co najmniej dwóch przedziałach, takich że liczby a i b nie należą do tego samgo przedziału.
Zad. 1. Po dodaniu ustalonej liczby a do każdej obserwacji nowa średnia będzie sumą poprzedniej średniej i liczby a. Podobnie po dodaniu ustalonej liczby a do każdej obserwacji nowa mediana będzie sumą poprzedniej mediany i liczby a. Natomiast wariancja nie zmieni się (dane zostana przesunięte, ale odległości między nimi będą zachowane, rozproszenie danych nie zmieni się). Wobec tego współczynik skośności zostanie pomnożony przez liczbę a.
Zad. 2. Po pomnożeniu każdej obserwacji przez niezerową liczbę a nowa średnia będzie iloczynem poprzedniej średniej i liczby a. Podobnie po pomnożeniu każdej obserwacji przez niezerową liczbę a nowa mediana będzie iloczynem poprzedniej mediany i liczby a. Natomiast wariancja zostanie pomnożona przez liczbę a2, a odchylenie standardowe przez liczbę |a| (odległości między danymi wzrosną/zmaleją a-krotnie, rozproszenie danych wzrośnie a-krotnie, wariancja mierzy kwadraty odległości). W takim razie współczynnik skośności zostanie pomnożony przez liczbę a/|a| = ±1, zatem pozostanie on niezmieniony (dla a>0) lub zmieni znak na przeciwny (dla a<0).
Zad. 3. Po dodaniu obserwacji x średnia wynosi
[tex]\frac{\frac{n(n+1)}{2}+x}{n+1}=\frac{n}{2}+\frac{x}{n+1}[/tex]
natomiast wariancja wynosi
[tex]\frac{\frac{n(n+1)(2n+1)}{6}+x^2}{n+1}-(\frac{n}{2}+\frac{x}{n+1})^2=\frac{n(2n+1)}{6}+\frac{x^2}{6(n+1)}-(\frac{n}{2}+\frac{x}{n+1})^2.[/tex]
Wygodnie jest zauważyć, że przed dodaniem x mediana była równa średniej, czyli [tex]\frac{n(n+1)}{2n}=\frac{n+1}{2}[/tex]. Niezależnie od parzystości n po dodaniu obserwacji x mediana wzrośnie o ½, zatem będzie wynosiła [tex]\frac{n+2}{2}=\frac{n}{2}+1[/tex]. Liczba x musi więc spełniać nierówności x>n oraz
[tex]\frac{\frac{x}{n+1}-1}{sqrt{\frac{n(2n+1)}{6}+\frac{x^2}{6(n+1)}-(\frac{n}{2}+\frac{x}{n+1})^2}}>c,[/tex]
co jest już wystarczającym rozwiązaniem zadania, gdyż pytano o warunekna x, nie precyzując, w jakiej postaci powinien być wyrażony. Ponieważ licznik ułamka po lewej stronie jest dodatni, możemy podnieść nierówność obustronnie do kwadratu i pomnożyć przez mianownik. Wówczas otrzymujemy nierówność kwadratową:
[tex](\frac{x}{n+1}-1)^2>c^2(\frac{n(2n+1)}{6}+\frac{x^2}{6(n+1)}-(\frac{n}{2}+\frac{x}{n+1})^2).[/tex]
Po uporządkowaniu przyjmuje ona postać:
[tex]\left[\frac{c^2+1}{(n+1)^2}-\frac{c^2}{6(n+1)}\right]x^2-\frac{c^2n+2}{n+1}x+\frac{c^2n^2}{4}-\frac{c^2n(2n+1)}{6}+1>0.[/tex]
W treści zadania podano, że poprzez zmianę x mamy uczynić współczynnik skośności większym od dowolnej liczby c, czyli de facto dowolnie dużym. Jest to sformułowanie na wyrost, ponieważ, jak się łatwo przekonać, analizując powyższą nierówność, w zależności od n można podać takie c, że nierówność ta nie zachodzi dla żadnego x>n.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
