W poprzednim odcinku ligi porównywaliśmy dwa zbiory obserwacji. W tym miesiącu powrócimy do tego tematu. Posłużymy się następującym przykładem:
Przykład 1. Porównujemy wyniki uzyskane w części matematycznej egzaminu gimnazjalnego przez chłopców i dziewczęta. Obliczenia przeprowadzamy w oparciu o dane dotyczące pięciu dziewcząt i czterech chłopców. Dziewczęta uzyskały następujące wyniki (w skali procentowej): 69, 73, 62, 67 i 75. Wyniki chłopców przedstawiają się następująco: 68, 61, 70 i 72.
Sporządźmy tabelę podobną do tej, jaką sporządzaliśmy w ubiegłym miesiącu, z tym że wartości odpowiadające poszczególnym wierszom uszeregujmy od największej do najmniejszej a wartości odpowiadające poszczególnym kolumnom od najmniejszej do największej. 1 oznacza, że wynik danej uczennicy jest większy od wyniku danego ucznia, natomiast 0 - na odwrót.
| ch\dz | 62 | 67 | 69 | 73 | 75 |
| 72 | 0 | 0 | 0 | 1 | 1 |
| 70 | 0 | 0 | 0 | 1 | 1 |
| 68 | 0 | 0 | 1 | 1 | 1 |
| 61 | 1 | 1 | 1 | 1 | 1 |
Widzimy, że ze względu na uporządkowanie wartości w wierszach i kolumnach zera i jedynki w powyższej tabeli nie są wymieszane, przeciwnie, obszary zajmowane przez zera i jedynki w powyższej tabeli są wyraźnie rozgraniczone.
Przypomnijmy, że aby obliczyć prawdopodobieństwo, że wynik losowo wybranej uczennicy jest wyższy od wyniku losowo wybranego ucznia, należy podzielić liczbę jedynek z powyższej tabeli przez iloczyn liczby dziewcząt i liczby chłopców. Prawdopodobieństwo to wynosi 11:(4·5)=11:20=0,55. Wprawdzie jest to liczba nieco większa od ½, ale dyskusyjnym byłoby przyznawanie palmy pierwszeństwa dziewczętom na podstawie takiego wyniku.
Okazuje się, że matematyczne postępowanie, jakie zostało przypomniane powyżej, może mieć ciekawą interpretację geometryczną.
Na podstawie wcześniej skonstruowanej tabeli zbudujmy jeszcze jedną tabelę. Będzie się ona składała z dwóch wierszy i tylu kolumn, z ilu składa się poprzednia tabela. Załóżmy, że poprzednia tabela zawierała k kolumn i m wierszy. W pierwszym wierszu nowej tabeli umieścimy liczby: 1/k, 2/k, …, k-1/k, 1. W drugim wierszu umieścimy sumę liczb z poszczególnych kolumn pierwszej tabeli podzieloną przez liczbę wszystkich wierszy w poprzedniej tabeli (czyli przez m). Następnie jeśli pierwsza kolumna nowej tabeli nie składa się z liczb 0 i 0, to dopisujemy te liczby jako pierwszą kolumnę nowej tabeli. Podobnie jeśli ostatnia jej kolumna nie składa się z liczb 1 i 1, to dopisujemy te liczby jako ostatnią kolumnę.
W naszym przykładzie w nowej tabeli w pierwszym wierszu umieścimy liczby: 1/5 = 0,2, 2/5 = 0,4, 3/5 = 0,6, 4/5 = 0,8, 1. Sumy liczb w kolejnych kolumnach wyjściowej tabeli wynoszą odpowiednio: 1, 1, 2, 4, 4, stąd w drugim wierszu nowej tabeli umieścimy liczby: 1/4 = 0,25, 1/4 = 0,25, 2/4 = 0,5, 4/4 = 1, 4/4 = 1. Następnie dopiszemy na początku kolumnę składającą się z zer.
| x | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| y | 0 | 0,25 | 0,25 | 0,5 | 1 | 1 |
Liczby w pierwszym wierszu będą pierwszymi współrzędnymi, a liczby w drugim wierszu - drugimi współrzędnymi punktów, które zaznaczymy w układzie współrzędnych. Po zaznaczeniu punktów łączymy je łamaną o odcinkach biegnących równolegle do osi układu współrzędnych w taki sposób, aby każdy punkt (poza pierwszym) był prawym końcem poziomego odcinka. W programie Gnumeric można to zrobić w następujący sposób:
1. Zaznaczamy nową tabelkę, na podstawie której chcemy narysować wykres i wybieramy Wstaw > Wykres lub odpowiednią ikonę z kolorowym wykresem.
2. Jako typ wykresu wybieramy ostatni na liście (XY).
3. Jako podtyp wybieramy szósty obrazek w kolejności. Przedstawia on "schodki" z zamalowanymi punktami na prawych końcach stopni.
4. Zatwierdzamy nasz wybór przyciskiem Wstaw. Następnie klikamy w arkuszu kalkulacyjnym w miejsce, gdzie chcemy umieścić wykres.
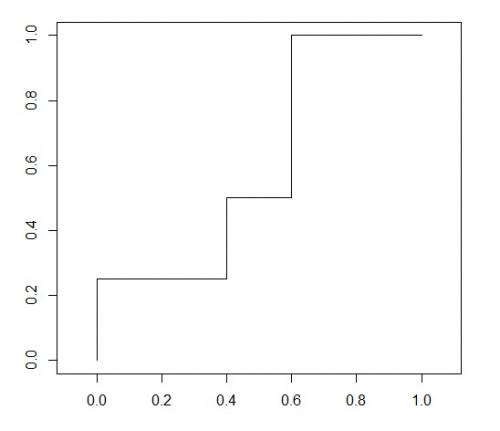
Warto odpowiednio rozciągnąć wykres, tak by proporcje jednostek na osiach były takie same. Zwróćmy uwagę, że współrzędne zaznaczonych punktów zawierają się w przedziale [0,1], a zatem cały wykres mieści się w kwadracie o wierzchołkach (0,0), (0,1), (1,1) i (1,0). Pole pod zaznaczoną krzywą jest równe obliczonemu wcześniej prawdopodobieństwu, że wynik losowo wybranej uczennicy jest wyższy od wyniku losowo wybranego ucznia.
Zaznaczona na wykresie linia nazywa się ODC (ang. ordinal dominance curve, krzywa dominacji porządkowej). Wykres ODC odpowiada ściśle tabeli, którą przedstawiliśmy w przykładzie na początku tych rozważań. Na jego podstawie można też obliczyć prawdopodobieństwo, że wynik losowo wybranej uczennicy jest wyższy od wyniku losowo wybranego ucznia. Prawdopodobieństwo to jest równe polu pod wykresem. Zwróćmy jednak uwagę, że sam wykres niesie jeszcze jedną interesującą informację.
Przypomnijmy, że porównanie między dwiema próbami, jakiego dokonujemy, opiera się na obliczeniu prawdopodobieństwa, że losowo wybrany pomiar z jednej grupy jest większy od losowego pomiaru z drugiej grupy. Jeśli prawdopodobieństwo to wynosi około ½, to nie możemy powiedzieć, że rozkłady danych są względem siebie uporządkowane. Jeśli dane w obu grupach leżą mnie więcej w tym samym miejscu (przy czym, jak powiedziano na początku, obserwacje się nie pokrywają), to linia ODC leży w pobliżu prostej o równaniu y = x (tę prostą łatwo można wyznaczyć, gdyż na wykresie zaznaczone są punkty leżące na niej: (0,0) i (1,1)). Nie jest to jednak jedyna możliwość, by pole obszaru pod łamaną wynosiło około ½.
Jeśli rozważylibyśmy dwa symetryczne zbiory danych o podobnych średnich ale różniące się wariancją, to okaże się, że prawdopodobieństwo, że obserwacja losowo wybrana z jednego zbioru jest większa od obserwacji losowo wybranej z drugiego zbioru, także jest bliskie ½. Teraz jednak dane w obu zbiorach nie leżą w tym samym miejscu, lecz dane z jednego zbioru są wyraźnie bardziej rozrzucone. Na wykresie wiąże się to z tym, że ODC nie leży już w pobliży prostej o równaniu y = x, lecz wyraźnie ją przecina, przy czym część nad i pod prostą o równaniu y = x są mają podobny kształt. Ponieważ podobna część łamanej leży powyżej i poniżej prostej o równaniu y = x, interesujące nas pole jest równe w przybliżeniu ½.
Widzimy zatem, że wykres ODC pozwala nam nie tylko obliczyć prawdopodobieństwo zachodzenia odpowiedniej nierówności między elementami losowo wybranymi spośród dwóch zestawów danych, ale również pozwala się zorientować bardziej szczegółowo, jak oba zbiory danych leżą względem siebie (co może się sprowadzać np. do porównywania wariancji).
W naszych rozważaniach musimy się zająć jeszcze jedną sytuacją, która w dotychczasowych rozważaniach była przez nas pomijana: jak porównywać pod względem prawdopodobieństwa dwa zbiory danych w sytuacji, gdy obserwacje mogą się powtarzać. Sytuację tę zilustruje poniższy przykład.
Przykład 2. Tym razem porównujemy wyniki części matematycznej egzaminu gimnazjalnego u ośmiu dziewcząt i pięciu chłopców. Dziewczęta uzyskały odpowiednio: 64, 67, 72, 73, 76, 80, 87 i 91 procent, chłopcy natomiast 61, 67, 73, 75, 84 procent. Wynikom poszczególnych dziewcząt będą odpowiadały kolumny, a wynikom poszczególnych chłopców - wiersze. Podobnie jak poprzednio w tabeli umieszczamy liczbę 1, gdy wynik danej uczennicy jest większy od wyniku danego ucznia, natomiast 0 gdy wynik danej uczennicy jest mniejszy od wyniku danego ucznia. Gdy uczeń i uczennica osiągnęli ten sam wynik, w komórce odpowiadającej takiej sytuacji umieszczamy liczbę ½.
| ch\dz | 64 | 67 | 72 | 73 | 76 | 80 | 87 | 91 |
| 84 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 75 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 73 | 0 | 0 | 0 | 0,5 | 1 | 1 | 1 | 1 |
| 67 | 0 | 0,5 | 1 | 1 | 1 | 1 | 1 | 1 |
| 61 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Gdy obserwacje mogą się powtarzać, w szczególności gdy możliwa jest sytuacja, że wynik danej uczennicy i wynik danego ucznia jest taki sam, obliczanie prawdopodobieństwa, że losowo wybrana uczennica uzyskała wynik wyższy od losowo wybranego ucznia, wydaje się niewystarczające. Wyobraźmy sobie sytuację, że zgromadziliśmy dane o tej samej licznie dziewcząt i chłopców, przy czym dobraliśmy uczniów w taki sposób, że można ich dobrać w pary złożone z uczennicy i ucznia, którzy uzyskali dokładnie ten sam wynik. Wówczas rozkład wyników u każdej z płci jest dokładnie taki sam. Mimo to prawdopodobieństwo, że wybrana uczennica uzyskała wynik wyższy od losowo wybranego ucznia, z pewnością będzie mniejsze niż ½.
W tej sytuacji rozsądniejsze wydaje się rozważanie sumy prawdopodobieństwa, że losowo wybrana uczennica uzyskała wynik wyższy od losowo wybranego ucznia, i połowy prawdopodobieństwa, że losowo wybrana uczennica i losowo wybrany uczeń uzyskali taki sam wynik. Suma ta jest równa sumie liczb z tabeli powyżej podzielonej przez iloczyn liczby wierszy i liczby kolumn w tabeli czyli podzielonej przez iloczyn liczby dziewcząt i liczby chłopców.
W naszym przykładzie suma prawdopodobieństwa, że losowo wybrana uczennica uzyskała wynik wyższy od losowo wybranego ucznia, i połowy prawdopodobieństwa, że losowo wybrana uczennica i losowo wybrany uczeń uzyskali taki sam wynik, wynosi zatem 25:(8·5)=0,625 (25 to suma liczb z tabeli).
Okazuje się, że taki sam wynik co przy użyciu tabeli możemy uzyskać, posługując się rangami. Musimy tylko odpowiednio zmodyfikować procedurę poznaną przed miesiącem. Jeśli wśród naszych danych występuje kilka obserwacji o takiej samej wartości, rangą dla takiej powtarzającej się obserwacji będzie średnia arytmetyczna numerów kolejnych, jakie powinny otrzymać te powtarzające się obserwacje.
W naszym przykładzie najgorszy wynik wyniósł 61 i otrzymuje on rangę 1. Następną w kolejności obserwacja wynosi 64, więc otrzymuje ona rangę 2. Kolejna wartość to 67. Występuje ona dwukrotnie. Można więc powiedzieć, że wartości 67 przypadają miejsca 3 i 4 w kolejności. Tej obserwacji przypisujemy więc rangę 3,5, co jest równe średniej arytmetycznej liczb 3 i 4. Liczba 72 występuje jeden raz i otrzymuje ona rangę 5. Kolejna obserwacja wynosi 73 i także występuje dwukrotnie, jest więc opatrzona rangą 6,5 (średnia arytmetyczna liczb 6 i 7). Rangi odpowiadające poszczególnym obserwacjom wypisano poniżej. Zaznaczono też, czy dany wynik należał do dziewczyny czy chłopaka
| grupa | ch | dz | ch | dz | dz | ch | dz | ch | dz | dz | ch | dz | dz |
| obserwacja | 61 | 64 | 67 | 67 | 72 | 73 | 73 | 75 | 76 | 80 | 84 | 87 | 91 |
| ranga | 1 | 2 | 3,5 | 3,5 | 5 | 6,5 | 6,5 | 8 | 9 | 10 | 11 | 12 | 13 |
Suma rang odpowiadających dziewczętom wynosi 2+3,5+5+6,5+9+10+12+13 = 61. Jeśli liczbę tę pomniejszymy o m(m+1)/2, gdzie m jest liczbą dziewcząt, otrzymamy 61-8·(8+1)/2 = 61-36 = 25 a więc tyle, ile wynosiła suma liczb we wcześniejszej tabeli.
czegółowo poznają studenci matematyki.
Zad. 1. Narysuj ODC dla porównania dwóch zestawów danych. Oblicz prawdopodobieństwo, że obserwacja losowo wybrana z pierwszego zestawu jest większa od dowolnej obserwacji z drugiego zestawu.
Zad. 2. Oblicz sumę prawdopodobieństwa, że obserwacja losowo wybrana z pierwszego zestawu danych jest większa od obserwacji losowo wybranej z drugiego zestawu danych, i połowy prawdopodobieństwa, że obserwacja losowo wybrana z pierwszego zestawu danych i obserwacja losowo wybrana z drugiego zestawu danych są równe.
Dane do zadań 1 i 2 znajdują się w tym pliku.
W obliczeniach pomocne może być w tym następujące wyrażenie:
=if(A2<B1;1;0)+if(A2=B1;0,5;0)
przyjmujące wartość 1, gdy liczba w komórce A2 jest mniejsza od liczby w komórce B1, wartość 0,5, gdy liczby w komórkach A2 i B1 są równe, oraz wartość 0, gdy liczba w komórce A2 jest większa od liczby w komórce B1 (odpowiednikiem funkcji if w polskie wersji Excela jest funkcja JEŻELI).
Zad. 3. Narysowano trzy wykresy ODC dla trzech par zestawów danych. Dopasuj dane do wykresów.
I)
| Zestaw I | Zestaw II | |
| Liczba obserwacji | 10 | 20 |
| Średnia | 13,02 | 11,95 |
| Wariancja | 1,88 | 1,94 |
II)
| Zestaw I | Zestaw II | |
| Liczba obserwacji | 15 | 25 |
| Średnia | 11,97 | 14,28 |
| Wariancja | 2,19 | 2,14 |
III)
| Zestaw I | Zestaw II | |
| Liczba obserwacji | 30 | 22 |
| Średnia | 14,39 | 15,61 |
| Wariancja | 1,88 | 9,11 |

Jako rozwiązanie zad. 1 i zad. 2 prześlij arkusz kalkulacyjny w formacje .gnumeric z przeprowadzonymi obliczeniami i wykresem, nadając mu nazwę postaci Imie_Nazwisko_czerwiec.gnumeric. Wszystkie ewentualne komentarze umieść w tym pliku.
Z zadaniami zaproponowanymi w czerwcowym etapie ligi najlepiej poradziła sobie Joanna Lisiowska, otrzymując 2,5 punktu. Kacper Toczek zdobył 1,5 punktu zaś Aleksandra Domagała - 1 punkt. Klasyfikacja generalna została podana w ramach listy nagrodzonych dostępnej tutaj.
Za rozwiązania zadań przeznaczonych na czerwiec Daria Bumażnik i Tomasz Stępniak otrzymują 2,5 punktu. Podsumowanie ligowych zmagań w ciągu całego roku szkolnego można znaleźć tutaj.
Zad. 1 i 2. Rozwiązanie zadań znajdują się w tym pliku.
Zad. 3. W (I) zarówno średnie jak i wariancje są porównywalne. Można się spodziewać, że ODC będzie leżeć w pobliżu prostej o równaniu y = x, co sugeruje rysunek C.
W (II) przy podobnej wariancji średnie są wyraźnie różne. Wobec tego możemy się spodziewać, że pole pod ODC będzie się znacznie rózniło od ½. Wniosek ten sugeruje rysunek A.
W (III) średnie są zbliżone, ale wariancje różnią się znacznie. Można przypuszczać, że pole pod ODC będzie zbliżone do ½, ale sama ODC wyraźnie będzie przecinać prostą o równaniu y = x. To sugeruje rysunek B.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


