W trójkącie można poprowadzić odcinek, który podzieli ten trójkąt na dwie figury o równym polu. Powiemy wtedy, że taka linia połowi pole lub że jest połowiącą pole.
W trójkącie można poprowadzić odcinek, który podzieli obwód tego trójkąta na dwie łamane o równej długości. Powiemy wtedy, że taka linia połowi obwód lub że jest połowiącą obwód.
Uruchamiając makra (ikona ![]() ),
możesz dorysować nowe połowiące.
),
możesz dorysować nowe połowiące.
Proponujemy do rozwiązania kilkanaście zadań (łatwych i trudniejszych).
Zadanie A.1.
W trójkącie równobocznym ABC, o boku a = 4,
niech PP' || AB będzie połowiącą pole.
Oblicz długość PP'. W jakim stosunku odcinek PP' dzieli środkową (wysokość) CD tego trójkąta?
Zadanie A.2.
W trójkącie równobocznym ABC, o boku a = 4,
niech QQ' || AB będzie połowiącą obwód.
Oblicz długość QQ'. W jakim stosunku odcinek QQ' dzieli środkową (wysokość) CD tego trójkąta?
Zadanie A.3.
W trójkącie prostokątnym ABC, o przyprostokątnych AC = BC = 4, niech PP' || AB będzie połowiącą pole. Oblicz długość PP'. W jakim stosunku odcinek PP' dzieli środkową (wysokość) CD tego trójkąta?
Zadanie A.4.
W trójkącie prostokątnym ABC, o przyprostokątnych AC = BC = 4, niech QQ' || AB będzie połowiącą obwód. Oblicz długość QQ'. W jakim stosunku odcinek QQ' dzieli środkową (wysokość) CD tego trójkąta?
Zadanie A.5.
W trójkącie ABC niech PP' || AB będzie połowiącą pole. W jakim stosunku odcinek PP' dzieli środkową CD tego trójkąta?
Zadanie A.6a.
W trójkącie równoramiennym ABC, AC = BC = 2, AB = 0,004, niech QQ' || AB będzie połowiącą obwód. W jakim stosunku odcinek QQ' dzieli środkową (wysokość) CD tego trójkąta?
Zadanie A.6b.
W trójkącie równoramiennym ABC, AC = BC = 2, AB =3,996, niech QQ' || AB będzie połowiącą obwód. W jakim stosunku odcinek QQ' dzieli środkową(wysokość) CD tego trójkąta?
Zadanie A.6c.
Czy jest taki trójkąt ABC, w którym połowiąca obwód QQ' || AB dzieli środkową CD na pół?
Zadanie A.7a. *
W trójkącie równoramiennym ABC, AC = BC,
PP' = 4 jest połowiąca pole, równoległą do AB
i QQ' = 3 jest połowiąca obwód, równoległą do AB.
a) Czy można obliczyć pole ![]() ABC ?
Jeśli tak, oblicz je.
ABC ?
Jeśli tak, oblicz je.
b) Czy można obliczyć obwód ![]() ABC ?
Jeśli tak, oblicz go.
ABC ?
Jeśli tak, oblicz go.
c) Czy można obliczyć długości boków ![]() ABC ?
Jeśli tak, oblicz je.
ABC ?
Jeśli tak, oblicz je.
Zadanie A.7b. *
W trójkącie ABC,
PP' = 4 jest połowiąca pole, równoległą do AB
i QQ' = 3 jest połowiąca obwód, równoległą do AB.
a) Czy można obliczyć pole ![]() ABC ?
Jeśli tak, oblicz je.
ABC ?
Jeśli tak, oblicz je.
b) Czy można obliczyć obwód ![]() ABC ?
Jeśli tak, oblicz go.
ABC ?
Jeśli tak, oblicz go.
c) Czy można obliczyć długości boków ![]() ABC ?
Jeśli tak, to oblicz je.
ABC ?
Jeśli tak, to oblicz je.
Zadanie B.1.
W ![]() ABC,
AB = 10, BC = 8 i AC = 6 niech AA' oznacza połowiącą pole i niech AA'' oznacza połowiącą obwód.
ABC,
AB = 10, BC = 8 i AC = 6 niech AA' oznacza połowiącą pole i niech AA'' oznacza połowiącą obwód.
a) Oblicz CA' : A'B .
b) Oblicz CA'' : A''B .
c) Oblicz długość AA' oraz AA'' .
Zadanie B.2.
W ![]() ABC,
AB = 10, BC = 8 i AC = 6
niech CC' oznacza połowiącą pole i niech CC'' oznacza połowiącą obwód.
ABC,
AB = 10, BC = 8 i AC = 6
niech CC' oznacza połowiącą pole i niech CC'' oznacza połowiącą obwód.
a) Oblicz AC' : C'B .
b) Oblicz AC'' : C''B .
c) Oblicz długość CC' oraz CC'' .
Zadanie B.3.
W trójkącie ostrokątnym ABC, niech CD oznacza wysokość. Uzasadnij, że jeśli połowiąca pole CC' pokrywa się z CD, to AC = BC.
Zadanie B.4.
W trójkącie ostrokątnym ABC, niech CD oznacza wysokość. Uzasadnij, że jeśli połowiąca obwód CC'' pokrywa się z CD, to AC = BC.
Zadanie B.5.
W trójkącie ostrokątnym ABC, niech CE oznacza odcinek dwusiecznej zawarty w trójkącie. Uzasadnij, że jeśli połowiąca pole CC' pokrywa się z CE, to AC = BC.
Zadanie B.6.
W trójkącie ostrokątnym ABC, niech CE oznacza odcinek dwusiecznej zawarty w trójkącie. Uzasadnij, że jeśli połowiąca obwód CC'' pokrywa się z CE, to AC = BC.
Zadanie B.7.
W trójkącie ABC niech CC' oznacza połowiącą pole i niech CC'' oznacza połowiącą obwód. Uzasadnij, że jeśli C' = C'', to AC = BC.
Zadanie B.8. *
W trójkącie ABC, niech:
CD oznacza wysokość,
CE oznacza odcinek dwusiecznej zawarty w trójkącie,
CC' oznacza połowiącą pole,
CC'' oznacza połowiącą obwód.
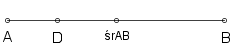
Na rysunku pokazano tylko bok AB.
Zaznacz punkty E, C', C''.
Uwaga. W rozwiązaniu niektórych z powyższych zadań przydatne może być twierdzenie o dwusiecznej:
Niech w trójkącie ABC punkt P leży na boku AB. Wtedy:
Zadanie C.1. *
W ![]() ABC
niech AA', BB', CC' oznaczają połowiące pole.
Uzasadnij, że odcinki AA', BB', CC' przecinają się w jednym punkcie.
ABC
niech AA', BB', CC' oznaczają połowiące pole.
Uzasadnij, że odcinki AA', BB', CC' przecinają się w jednym punkcie.
Zadanie C.2. *
W ![]() ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód. Uzasadnij, że odcinki AA'', BB'', CC'' przecinają się w jednym punkcie.
ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód. Uzasadnij, że odcinki AA'', BB'', CC'' przecinają się w jednym punkcie.
Zadanie C.3. *
W ![]() ABC
niech AA', BB', CC' oznaczają połowiące pole
i niech S oznacza punkt wspólny tych trzech odcinków. Uzasadnij, że nie istnieje czwarta połowiąca pole przechodząca przez S.
ABC
niech AA', BB', CC' oznaczają połowiące pole
i niech S oznacza punkt wspólny tych trzech odcinków. Uzasadnij, że nie istnieje czwarta połowiąca pole przechodząca przez S.
Zadanie C.4. *
W ![]() ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód i niech T oznacza punkt wspólny tych trzech odcinków.
ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód i niech T oznacza punkt wspólny tych trzech odcinków.
Uzasadnij, że nie istnieje czwarta połowiąca obwód przechodząca przez T.
Zadanie C.5. *
Czy punkt wewnętrzny trójkąta może być punktem wspólnym czterech połowiących pole?
Zadanie C.6. *
Czy punkt wewnętrzny trójkąta może być punktem wspólnym czterech połowiących obwód?
Uwaga.
W rozwiązaniu niektórych z powyższych zadań przydatne może być twierdzenie Cevy:
Niech w trójkącie ABC punkt Co leży na boku AB,
Ao leży na boku BC i
Bo leży na boku AC.
Wtedy:
wtedy i tylko wtedy, gdy
odcinki AAo, BBo, CCo przecinają się w jednym punkcie.
Zadanie D.1.
Czy każde dwie połowiące pole trójkąta ABC muszą się przecinać?
Zadanie D.2.
Czy każde dwie połowiące obwód trójkąta ABC muszą się przecinać?
Zadanie D.3.
Uzasadnij, że w trójkącie ABC odcinek QQ' połowi obwód wtedy i tylko wtedy, gdy dzieli ten trójkąt na dwa trójkąty o równych obwodach.
Zadanie D.4.
Czy połowiąca obwód może nie przecinać pewnej połowiącej pole?
Zadanie D.5.
W ![]() ABC
niech AA', BB', CC' oznaczają połowiące pole.
ABC
niech AA', BB', CC' oznaczają połowiące pole.
Czy ![]() A'B'C'
jest podobny do
A'B'C'
jest podobny do ![]() ABC ?
ABC ?
Zadanie D.6.
W ![]() ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód.
ABC
niech AA'', BB'', CC'' oznaczają połowiące obwód.
Czy ![]() A''B''C''
jest podobny do
A''B''C''
jest podobny do ![]() ABC ?
ABC ?



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


