Wizualizacja danych - histogram

Nazwa histogram pochodzi od dwóch łacińskich rzeczowników: histos (rzeczy pionowe) oraz gramma (zapisywanie). Dane statystyczne są w nim prezentowane za pomocą pionowych słupków. Prekursorem tego sposobu wizualizacji był angielski matematyk i statystyk Karl Pearson, który wykorzystał taki diagram w swej pracy z 1891 roku.

Do czego stosujemy histogram, a do czego nie
Histogram służy do prezentacji rozkładu danych, które są zmiennymi ciągłymi, tzn. mogą przyjmować wiele wartości liczbowych należących do pewnego zakresu (w odróżnieniu od danych kategorycznych, które przyjmują jedną ze ściśle określonego zbioru wartości, np. płeć, miesiąc urodzenia lub ocena roczna). Zmienną ciągłą może być np. wzrost człowieka (wartość z przedziału 50-260 cm) lub czas poświęcony na przygotowanie śniadania mierzony w pełnych minutach (liczba od 2 do 60). Dobrze opracowany histogram pozwala łatwo zobaczyć, jak dane się rozkładają się w całym zakresie ich zmienności i czy jest jakiś przedział lub przedziały, do których obserwacje wpadają najczęściej lub najrzadziej.

Czym histogram różni się od diagramu słupkowego
Zarówno w histogramie i w diagramie słupkowym rysujemy prostokątne słupki. Różnica polega na tym, że histogram stosujemy do prezentacji rozkładu zmiennych ciągłych, a wykres słupkowy do zmiennych kategorycznych. Dlatego w wykresie słupkowym należy zrobić odstęp pomiędzy kolejnymi słupkami, a w histogramie kolejny słupek styka się pionowym bokiem z poprzednim. To gwarantuje, że nie pominiemy danych z żadnego przedziału w obrębie zakresu tych danych.

rysunek 1

Cechy histogramu
W poniższym przykładzie nie wiemy, jakich danych dotyczy diagram, ale i tak możemy odczytać z niego pewne informacje. Przypomnijmy, że moda to wartość najczęściej występująca w danym zestawie danych. Z diagramu łatwo widzimy, że najczęściej przyjmowane są wartości z przedziału [2,3). Diagram taki nazywamy jednomodalnym, bo występuje w nim tylko jeden słupek, który jest znacząco wyższy od pozostałych. Co prawda tyle samo obserwacji należy do przedziału [1,2) co do przedziału [3,4) wokół najwyższego słupka, ale zdecydowanie więcej obserwacji wypada na prawo od niego niż na lewo. Dane nie rozkładają się więc symetrycznie wokół mody.

Jak poprawnie wykonać histogram
Histogram składa się z prostokątnych słupków o równej szerokości i różnych wysokościach narysowanych w prostokątnym układzie współrzędnych. Jak taki diagram wykonać?

• Narysuj prostopadłe osie układu współrzędnych.
• Wśród danych znajdź wartości najmniejszą i największą. Dzięki temu ustalisz zakres zmienności danych na osi x.
• Podziel ten zakres na rozłączne przedziały równej długości, sumujące się do całego zakresu (dzięki temu słupki histogramu będą miały równą szerokość). Zazwyczaj rozłączność przedziałów na osi x uzyskuje się w ten sposób, że wszystkie przedziały poza ostatnim bierze się lewostronnie domknięte, a prawostronnie otwarte, natomiast ostatni przedział bierze się domknięty obustronnie. Można też wziąć pierwszy przedział obustronnie domknięty, a pozostałe - lewostronnie otwarte i prawostronnie domknięte. Nie ma tu sztywnych reguł, bo za każdym razem dopasowujemy wybór przedziałów do danych, jakie chcemy prezentować na diagramie.
• Im więcej jest danych, tym więcej przedziałów możesz utworzyć. Im większy jest rozstęp danych (różnica między wartościami największą i najmniejszą), tym dłuższe mogą być przedziały.
• Na na osi y odnotuj liczby obserwacji wpadających do danego przedziału (ta liczba jest odpowiedzialna za wysokość słupka). Policz, ile razy wartości danych wpadały do poszczególnych (wydzielonych na osi x) przedziałów i narysuj nad każdym przedziałem na osi x słupek o takiej właśnie wysokości.
• Podpisz osie diagramu, żeby było jasne, jakie wartości są na nich zaznaczone (oś pozioma zawiera nazwę zmiennej, a pionowa - liczbę obserwacji). Pamiętaj o podaniu jednostki na osi x, w jakich dane są wyrażone (np. czas w minutach, wzrost w centymetrach). Dobór jednostki na osi y zależy od liczby obserwacji (sztuki, setki sztuk, tysiące, miliony).
• Nadaj histogramowi tytuł, który będzie informował o tym, czego dotyczą zebrane dane.
• Przeanalizuj kształt histogramu, opisz jego własności i wyciągnij z nich wnioski. Możesz postawić dalsze hipotezy wymagające dokładniejszego zbadania. 

Przykład 1. Nobliści z ekonomii
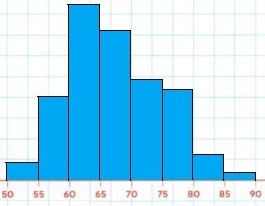
Wykonaj histogram dotyczący wieku laureatów Nagrody Banku Szwecji im. Alfreda Nobla z nauk ekonomicznych.

Dane:

Obliczenia:

• Wśród danych znajdujemy najmniejszy i największy wiek noblistów - 51 i 89 lat. Zatem zakres na osi x wystarczy ustalić pomiędzy 50 i 90, gdyż nie mamy obserwacji spoza tego przedziału. Na histogramie oś pozioma nie musi zaczynać się od zera. Jednak jeśli zaczniemy oś poziomą od 20 (wiek, w którym na ogół kończy się wykształcenie powszechne), dobitnie pokażemy, że wśród laureatów nagrody Nobla z ekonomii nie ma ludzi młodych.
• Ustalmy podział zakresu danych na 5-letnie przedziały: [50, 55), [55, 60), [60, 65), [65, 70), [70, 75), [75, 80), [80, 85), [85, 90].
• Policzmy obserwacje, które wpadają do poszczególnych przedziałów:
  [50, 55): 53, 51 - 2 sztuki
  [55, 60): 56, 57, 55, 58, 56, 56, 58, 58, 56, 55 - 10 sztuk,
  [60, 65): 61, 61, 61, 61, 61, 61, 64, 62, 64, 60, 63, 60, 63, 62, 63, 63, 62, 63, 64, 62, 64 - 21 sztuk,
  [65, 70): 68, 69, 67, 67, 68, 68, 69, 67, 66, 65, 67, 67, 67, 67, 66, 68, 67, 65 - 18 sztuk,
  [70, 75): 70, 71, 74, 70, 73, 73, 74, 71, 71, 74, 70, 70 - 12 sztuk,
  [75, 80): 75, 75, 76, 77, 77, 77, 78, 75, 76, 70, 78 - 11 sztuk,
  [80, 85): 84, 82, 81 - 3 sztuki,
  [85, 90]: 89 - 1 sztuka.
• Warto sprawdzić, czy nie pomyliliśmy się przy zliczaniu obserwacji. Wyniki ze wszystkich grup powinny sumować się do liczby 77 laureatów, 2+10+21+18+12+11+3+1 = 77.
• Podpisujemy osie układu: pionową jako „liczba laureatów”, a poziomą - „wiek laureatów w latach”, rysujemy słupki, nadajmy tytuł diagramowi.

Histogram:

Wnioski:
Łatwo zaobserwować, że najwięcej laureatów ma od 60 do 65 lat, trochę mniej jest w wieku od 65 do 70 lat, a całkiem mało w wieku od 50 do 55 lat i od 85 do 90 lat.
Oczywiście trudno dostać nagrodę w wieku powyżej 85 lat, bo wielu potencjalnych kandydatów nie dożywa do tego czasu. Najczęściej nagrodę otrzymuje się pomiędzy 55 a 80 rokiem
życia, czyli wiele lat po dokonaniu odkrycia, za które nagroda jest przyznawana (takich odkryć dokonują zazwyczaj ludzie młodzi). Możemy stad wyciągnąć wniosek, że Nagroda Banku Szwecji w dziedzinie nauk ekonomicznych nie jest przyznawana pochopnie, za stosunkowo świeże wyniki. Musi
minąć sporo czasu, zanim świat nauki przyswoi takie odkrycie i
dostrzeże jego ważną rolę dla rozwoju wiedzy i zanim okaże się, jak duże korzyści przyniosło ono ludzkości.

Przykład 2. Wyniki sprawdzianu z matematyki
W klasie liczącej 24 uczniów został przeprowadzony sprawdzian z matematyki składający się z pięciu zadań, każde było oceniane w skali 0-5 pkt. Dodatkowo można było otrzymać 1 punkt za podpunkt z (*) w ostatnim zadaniu. Po sprawdzeniu prac nauczyciel zauważył, że sprawdzian w tej klasie nie poszedł najlepiej. Postanowił stworzyć histogram, by łatwiej wyciągnąć wnioski. Zrób to i ty.

Dane:
maksymalna liczba możliwych do uzyskania punktów: 26
liczba uczniów piszących sprawdzian: 24
wyniki uczniów: 9 pkt, 11 pkt, 18 pkt, 17 pkt, 6 pkt, 2 pkt, 5 pkt, 15 pkt, 14 pkt, 16 pkt, 17 pkt, 6 pkt, 19 pkt, 12 pkt, 13 pkt, 5 pkt, 17 pkt, 18 pkt, 4 pkt, 14 pkt, 17 pkt, 19 pkt, 5 pkt, 16 pkt.

Obliczenia:

• Wartość najmniejsza 2 pkt, wartość największa 19 pkt, rozstęp danych 17.
  Moglibyśmy zakres osi poziomej ustalić na 2-19, ale lepszy będzie zakres 0-26, gdyż wyraźnie zobaczymy, że nie było obserwacji wpadających do skrajnych przedziałów.
• Utwórzmy przedziały długości 2 i policzmy, ile wyników wpada do każdego z nich.
  [0, 2): 0 wyników,
  [2, 4): 1 wynik,
  [4, 6): 4 wyniki,
  [6, 8): 2 wyniki,
  [8, 10): 1 wynik,
  [10, 12): 1 wynik,
  [12, 14): 2 wyniki,
  [14, 16): 3 wyniki,
  [16, 18): 6 wyników,
  [18, 20): 4 wyniki,
  [20, 22): 0 wyników,
  [22, 24): 0 wyników,
  [24, 26]: 0 wyników.
• Na osi y jako jednostkę obieramy 1, gdyż nie mamy dużo obserwacji wpadających do jednego przedziału (maksymalnie 6). Oś y podpiszemy jako „liczba uczniów”, a oś x jako „liczba punktów”.

Histogram:

Wnioski:
Wyniki sprawdzianu były dość zróżnicowane. Widzimy, że histogram jest dwumodalny, ma dwa lokalne maksima w przedziałach [4,6) oraz [16,18). Wykres przypomina dwie górki połączone obniżeniem. Większa część klasy poradziła sobie dobrze z zadaniami (uzyskali więcej niż połowę możliwych punktów), ale wiele osób uzyskało bardzo słabe wyniki (aż 1/3 uczniów nie uzyskała nawet 10 punktów) i nikt nie uzyskał więcej niż 20 punktów. Zapewne nauczyciel nie spodziewał się takich wyników, ponieważ zazwyczaj bywa tak, że najwięcej jest wyników średnich, a tych dobrych i słabych jest mniej i występują w podobnych liczbach (histogram jest wówczas symetryczny wokół swojej mody). W tym przykładzie wyników zbliżonych do połowy możliwych punktów jest stosunkowo mało. Dlaczego? Możliwe, że sprawdzian był źle skonstruowany. Mógł zawierać tylko zadania (za)łatwe i (za)trudne, bez zadań pozwalających rozstrzelić uczniów średnich. Słabsi i średni uczniowie poradzili sobie z tylko z łatwymi zadaniami, uczniowie najlepsi nie rozwiązali najtrudniejszych zadań. Były one za trudne dla najlepszych uczniów tej klasy. Inną przyczyną takiego rozkładu wyników mogła być niewystarczająca ilość czasu na rozwiązanie wszystkich zadań przez najlepszych uczniów.

Modyfikacja:
Jak wyglądałby powyższy histogram, gdyby przyjąć na osi x przedziały innej długości, np. co 5 punktów, przy czym, ponieważ nikt go nie zrobił, anulujemy zadanie z (*) i podzielimy 25 punktów na przedziały: [0, 5), [5, 10), [10, 15), [15, 20), [20, 25].
Wtedy wpada do nich odpowiednio 2, 6, 5, 11 i 0 obserwacji. Teraz histogram wyglada jak poniżej.

Wnioski:
Znowu zauważamy, że nikt nie uzyskał więcej niż 20 punktów, jednak zgubiliśmy informację na temat tego, czy były prace bardzo słabe, np. ocenione na 0 pkt. (widzimy tylko, że 2 osoby uzyskały liczbę punktów z przedziału od 0 do 5).
Kształt wykresu przypomina wznoszące się schody i istotnie różni się od wcześniejszego. Wydaje się, że mniej więcej tyle samo osób uzyskało wyniki poniżej, co powyżej 50% możliwych punktów. Jakie teraz wnioski mógłby wyciągnąć nauczyciel? Czy uczniowie poradzili sobie z zadaniami zgodnie z jego oczekiwaniami? Czy zadania były zaplanowane poprawnie? Jaką szerokość przedziału można przyjąć za optymalną? Czy bardziej precyzyjne informacje otrzymamy przy mniejszych, czy większych ich szerokosciach?

Przykład 4. Długie rzeki w Polsce
Poniższe dane przedstawiają długość w kilometrach rzek w Polsce nie krótszych niż 99 km.

Dane:
Wisła - 1047 km
Odra - 854 km
Warta - 808 km
Bug - 772 km
Narew - 484 km
San - 458 km
Noteć - 391 km
Pilica - 319 km
Wieprz - 303 km
Dunajec - 247 km
Bóbr - 272 km
Łyna - 264 km
Nysa Łużycka - 252 km
Wkra - 249 km
Brda - 238 km
Prosna - 217 km
Drwęca - 207 km
Wisłok - 205 km
Wda - 198 km
Drawa - 186 km
Nysa Kłodzka - 182 km
Poprad - 170 km
Pasłęka - 169 km
Rega - 168 km
Bzura - 166 km
Wisłoka - 164 km
Obra - 164 km
Lega - 157 km
Biebrza - 155 km
Wierzyca - 151 km
Nida - 151 km
Gwda - 145 km
Czarna Hańcza - 142 km
Liwiec - 142 km
Orzyc - 142 km
Wieprza - 140,3 km
Barycz - 139 km
Parsęta - 139 km
Słupia - 138,6 km
Kamienna - 138 km
Ner - 134 km
Mała Panew - 132 km
Raba - 132 km
Omulew - 127 km
Kwisa - 126 km
Ina - 126 km
Krzna - 120 km
Wełna - 118 km
Radomka - 116 km
Skrwa - 114 km
Ełk - 113 km
Wel - 107 km
Radunia - 103 km
Szkwa - 103 km
Netta - 102 km
Supraśl - 102 km
Nurzec - 100 km
Oława - 99,01 km.

Obliczenia:

• wartość najmniejsza 99,01 km, wartość największa 1047 km, rozstęp danych 948.
  Przedziały na osi x powinny być stosunkowo duże, aby nie było tak, że wiele przedziałów nie będzie zawierało żadnej obserwacji.
• Podzielmy więc zakres wartości od 0 do 1050 na przedziały długości 50 km i zliczmy wpadające do tych przedziałów rzeki:
  [0, 50): 0 rzek,
  [50, 100): 1 rzeka,
  [100, 150): 26 rzek,
  [150, 200): 13 rzek,
  [200, 250): 6 rzek,
  [250, 300): 3 rzeki,
  [300, 350): 2 rzeki,
  [350, 400): 1 rzeka,
  [400, 450): 0 rzek,
  [450, 500): 2 rzeki,
  [500, 550): 0 rzek,
  [550, 600): 0 rzek,
  [600, 650): 0 rzek,
  [650, 700): 0 rzek,
  [750, 800): 1 rzeka,
  [800, 850): 1 rzeka,
  [850, 900): 1 rzeka,
  [900, 950): 0 rzek,
  [950, 1000): 0 rzek,
  [1000, 1050]: 1 rzeka,
  liczba obserwacji w poszczególnych przedziałach sumuje się do 58, co zgadza się z liczbą rozpatrywanych rzek.
• Na osi x zaznaczmy jednostkę równą 50, a na osi y równą 2, bo rozbieżność liczby obserwacji w jednym przedziale jest dość duża (od 0 do 26). Oś poziomą opiszmy jako „długość rzeki w km”, a oś pionową jako „liczba rzek”.

Histogram:

Wnioski:
Czy z tego histogramu wynikają jakieś interesujące wnioski? Widzimy, że największa liczba rzek ma długość między 100 a 150 kilometrów. Typowe długości rzek należą do przedziału od 50 do 500 km. Mamy także do czynienia z wartościami odstającymi - rzeki o długości powyżej 750 km. Jest bardzo mało takich rzek i ich długości mocno różnią się od pozostałych.
Trudno tu wyciągnąć jakies istotne wnioski i nie bardzo wiadomo, jakiemu celowi miałaby ta wizualizacja danych służyć. Ten przykład pokazuje, że przy tworzeniu histogramu trzeba mieć konkretny cel badawczy, który chcemy zilustrować lub przeanalizować.Jakie hipotezy dotyczącepolskich rzek można by zbadać uwzględniając być może jakieś dodatkowe o nich informacje?

Wady i zalety histogramów
Należy pamiętać, że wybór diagramu do wizualizacji danych statystycznych zależy od tego, jakiego typu mamy dane i jakie zależności chcemy przedstawić. Także histogramy mają swoje plusy i minusy. Jedne informacje łatwo z nich odczytać, inne trudniej, a w przypadku jeszcze innych jest to całkowicie niemożliwe.

Zalety histogramu to:

• duża prostota i popularność,
• duża czytelność (nawet dla uczniów nie potrafiących jeszcze wprawnie czytać i liczyć),
• łatwość wykonania (nawet w młodszych klasach SP, wystarczy posiadać podstawy rachunków na liczbach naturalnych),
• dobra ilustracja problemu rozkładu pewnej cechy,
• łatwość porównania diagramów tej samej cechy dla różnych pupulacji,
• możliwość łatwego zauważenia wartości skrajnych i typowych oraz wielomodalności danych.

Wady histogramu to:

• subiektywny wybór liczby przedziałów,
  co wiąże się z niejednoznacznością kształtu diagramu, a to daje możliwość manipulowania wnioskami,
• brak możliwości łatwego odczytania takich wartości statystycznych jak średnia, mediana i inne kwartyle,
• konieczność zebrania odpowiednio dużej liczby danych.,
• brak możliwości przedstawienia korelacji danych.

Zastosowanie w szkole:

• rachunki na liczbach całkowitych,
• wprowadzenie i wykorzystanie układu współrzędnych na płaszczyźnie,
• zbieranie, analiza, wizualizacja danych, prowadzenie wnioskowań statystycznych,
• integracja nauczania matematyki z innymi dyscyplinami (historia, geografia, przyroda, ekonomia),
• wprowadzenie na lekcjach różnych przedmiotów elementów statystyki,
• wprowadzenie na lekcjach matematyki elementów historii statystyki,
• tworzenie infografik na potrzeby projektów i codziennego życia szkolnego,
• wykorzystanie arkusza kalkulacyjnego lub kalkulatora graficznego do automatycznego przygotowania diagramu.

Histogramy w tym artykule wykonano w arkuszu kalkulacyjnym MS Excel. Warto jednak podkreślić, że początkowo wykonywanie diagramów kredkami na papierze (w kratkę lub milimetrowym) ma znaczne walory kształcące i poznawcze, pozwala też lepiej zrozumieć istotę histogramu. Histogram wykonywany automatycznie pomija etap obliczeń i projektowania wyglądu diagramu.

Źródła:

• E. Baranowska, P. Biecek, P. Sobczyk, Wykresy unplugged, Wydawnictwo Uniwersytetu Warszawskiego, Warszawa 2018
• https://mathshistory.st-andrews.ac.uk/Biographies/Pearson/