Jednym z najpopularniejszych sposobów prezentowania danych statystycznych jest diagram kołowy. Często można spotkać go np. w reklamach, sondażach wyborczych, podręcznikach z różnych przedmiotów i wielu innych sytuacjach. Przedstawia on względny udział danej części w całości.
Jednym z najpopularniejszych sposobów prezentowania danych statystycznych jest diagram kołowy. Często można spotkać go np. w reklamach, sondażach wyborczych, podręcznikach z różnych przedmiotów i wielu innych sytuacjach. Przedstawia on względny udział danej części w całości.
Jako pierwszy takiego diagramu do prezentacji danych użył na początku XIX wieku szkocki inżynier i statystyk William Playfair. Nazwał go "pie chart" czyli diagram plackowy, co nawiązuje do kształtu popularnego brytyjskiego ciasta (tarty z owocami) i dobrze oddaje istotę tego wykresu.
Zaletami diagramu kołowego są jego popularność, prostota oraz czytelność. Każdy (nawet dziecko nie potrafiące jeszcze sprawnie czytać ani liczyć) jest w stanie jednym rzutem oka zrozumieć, co taki diagram przedstawia i jakie z tego wynikają wnioski. Dobrze oddaje on strukturę części pewnej całości, np. udział snu w innych czynnościach w ciągu doby, udział osób z zadanej grupy wiekowej w wyborach prezydenckich itp. Jednocześnie ten typ diagramu bywa kontrowersyjny, gdyż jego wymowa zależy często od tego, w jaki sposób sklasyfikujemy prezentowane dane w grupy.
Przykład 1. Podział czasu ucznia w ciągu doby
Dane:
| czynności | liczba godzin |
| sen | 9 |
| szkoła | 8 |
| czas wolny | 6 |
| obowiązki domowe | 1 |
Diagram kołowy:

Wnioski:
Jednym rzutem oka można ocenić, że najwięcej czasu w ciągu doby statystyczny uczeń poświęca na sen (ponad 1/3 czasu), ale porównywalnie dużo czasu spędza w szkole (1/3 czasu) i w domu (trochę mniej niż 1/3). Obowiązki domowe zajmują mu niewiele czasu, a czwartą część doby spędza, rozwijając zainteresowania wg własnych upodobań. Przy projektowaniu ankiety warto byłoby wprowadzić dwie kategorie czasu wolnego: czas spędzany na świeżym powietrzu lub na aktywności fizycznej oraz czas poświęcony na odrabianie lekcji i przygotowanie się do szkoły. Wtedy wyniki mogłyby prowadzić do znacznie ciekawszych wniosków.
Ponieważ wykres kołowy pokazuje udział części w całości, jest nieprzydatny do wizualizacji dwóch serii danych.
Przykład 2. Podział czasu ucznia w ciągu doby
Dane:
| czynności | liczba godzin |
| sen | 9 |
| szkoła: matematyka j. polski j. angielski WF inne |
8: 2 2 1 1 2 |
| czas wolny | 6 |
| obowiązki domowe | 1 |
Diagram kołowy:
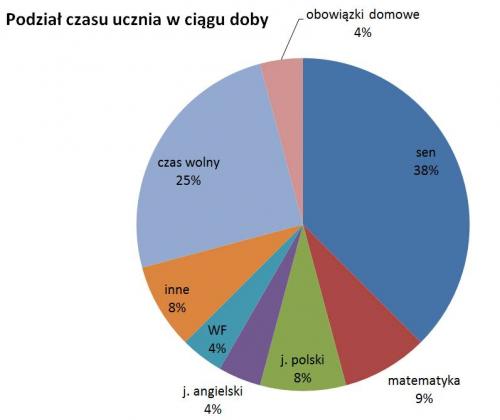
Wnioski:
W tym przykładzie na jednym diagramie umieszczono serie danych różnych typów i nie daje to klarownego obrazu sytuacji. Każdą serię należało przedstawić na osobnym diagramie, np. "podział czasu ucznia w ciągu doby" oraz "podział czasu ucznia w szkole". Przykład ten pokazuje też, że diagram kołowy będzie też nieprzydatny, gdy na wykresie będzie dużo pól o niewielkim udziale w całości danych (dużo wąskich wycinków). Dlatego przed wykonaniem wykresu ważne jest, aby dane mądrze sklasyfikować i pogrupować. Czy potrafisz wyjaśnić, dlaczego matematyka zajmuje 9% diagramu, skoro z danych liczbowych wynika, że zajmuje tę samą część doby, co język polski i inne przedmioty?
Zadanie 1. Wykonaj diagram własnego podział czasu w ciągu doby. Porównaj go z przykładami zaprezentowanymi wyżej. Jakie wnioski nasuwają się po analizie Twojego diagramu? Czy warto coś zmienić w Twoim rozkładzie dnia?
Diagram kołowy jest też nieprzydatny wówczas, gdy interesują nas np. wyniki wyborów, a występują w nich zbliżone wartości udziałów kilku kandydatów. Nie tylko trudno jest wówczas zobaczyć wprost z diagramu, kto wygrał, ale nawet podanie wartości procentowych dla poszczególnych pól może nie dać rozstrzygnięcia ze względu na błędy zaokrągleń przy niewielkiej różnicy wartości danych.
Przykład 3. Wyniki wyborów na przewodniczącego samorządu uczniowskiego
Dane:
| kandydat | liczba głosów |
| Alicja Nowacka | 136 |
| Dominik Adamski | 129 |
| Jan Klimek | 125 |
| Patrycja Wita | 34 |
Diagram kołowy:

Wnioski:
Z diagramu trudno odczytać, kto zwyciężył w wyborach, a procentowe udziały głosów uzyskanych przez dwóch kandydatów są równe, mimo że uzyskali inne liczby głosów.
Jak poprawnie stosować diagram kołowy
- Wybierz zagadnienie, w którym badany jest udział części w całości.
- Unikaj zagadnień, w których istotne są precyzyjne wartości udziałów części w całości.
- Użyj jednego typu danych sklasyfikowanych w adekwatne dla tematu diagramu grupy.
- Unikaj zbyt wielu grup o niewielkich udziałach w całości, wybieraj raczej zagadnienia o dobrze widocznym udziale każdej części w całości.
Jak poprawnie wykonać diagram kołowy
- Postaw pytanie badawcze dotyczące podziału pewnej całości na części.
- Dowiedz się lub oblicz, ile wynosi całość w rozważanym problemie i w jakich jednostkach jest wyrażona.
- Zbierz potrzebne dane w tych samych jednostkach i sklasyfikuj je w grupy adekwatne do tematu badania. Nadaj nazwy tym grupom.
- Nadaj diagramowi tytuł zgodny z tematem badania.
- Ustal, jaki ułamek/procent całości stanowi każda z części.
- Ustaw części w logicznej kolejności (np. wg rosnących wartości ułamków, chronologicznie, alfabetycznie lub w innej naturalnej kolejności)
- Dla każdego z otrzymanych ułamków oblicz, ile stopni ma taki ułamek kąta pełnego (czyli ile wynosi taki ułamek liczby 360).
- Odmierz kątomierzem otrzymane liczby stopni w kole, zaczynając od kierunku pionowego zwróconego w górę (godz. 12 na zegarze).
- Każdą z części koła zamaluj kontrastowym kolorem.
- Każdą z części koła opisz nazwą danej części całości i podaj odpowiadający tej części ułamek całości.
Przykład 4. Powierzchnia Ziemi
Dane:
| typ terenu | powierzchnia w km2 |
| ląd | 148 940 000 |
| woda | 361 132 000 |
Obliczenia:
- całkowita powierzchnia Ziemi: 148 940 000 + 361 132 000 = 510 072 000 km2
- część Ziemi zajmowana przez ląd: 361132000 : 510072000 ≈ 0,708, czyli ok. 71%
- część Ziemi zajmowana przez wodę: 1–0,708 = 0,292, czyli ok. 29%
- kąt reprezentujący na diagramie ląd: 0,71·360° = 255,6°
- kąt reprezentujący na diagramie wodę: 360°–255,6° = 104,4°
Diagram kołowy:

Wnioski:
Jednym rzutem oka widać, że zdecydowanie większą część powierzchni Ziemi zajmują morza i oceany (ponad 2/3), natomiast lądy to mniej niż 1/3 całkowitej powierzchni Ziemi.
Przykład 5. Wyniki ankiety szkolnej "Czy lubisz filmy fantasy"
Dane:
| wybrana odpowiedź | liczba głosów |
| tak | 56 |
| nie | 34 |
| nie mam zdania | 13 |
Obliczenia:
- liczba oddanych głosów: 56+34+13 = 103
- część głosów oddanych na "tak": 56:103 ≈ 0,5437, czyli ok. 54%
- część głosów oddanych na "nie": 34:103 ≈ 0,3301, czyli ok. 33%
- część głosów oddanych na "nie mam zdania": 13:103 ≈ 0,1262, czyli ok. 13%
- kąt odpowiadający na diagramie głosom na "tak": 0,54·360° = 194,4°
- kąt odpowiadający na diagramie głosom na "nie": 0,33·360° = 118,8°
- kąt odpowiadający na diagramie głosom "nie mam zdania": 360°–194,4°–118,8° = 46,8°
Diagram kołowy:

Wnioski:
Jednym rzutem oka widać, że w tej szkole zdecydowana większość uczniów zna filmy fantasy i ma na ich temat wyrobioną opinię: ponad połowa uczniów lubi je, a trzecia część uczniów jest przeciwnikami filmów o takiej tematyce.
Przykład 6. Koszt balu karnawałowego na 50 par
Dane:
| rodzaj wydatku | koszt w zł |
| wynajem sali | 8 000 |
| catering | 10 000 |
| DJ | 5 500 |
| fotograf | 3 200 |
| inne (dekoracje, kotyliony) | 2 500 |
Obliczenia:
- całkowity koszt przygotowania imprezy: 8000+10000+5500+3200+2500 = 29200 zł
- catering: 8000:29200 ≈ 0,274, czyli ok. 27%, co daje kąt 0,27·360° = 97,2°
- wynajem sali: 10000:29200 ≈ 0,3425, czyli ok. 34%, co daje kąt 0,34·360° = 122,4°
- DJ: 5500:29200 ≈ 0,1884, czyli ok. 19%, co daje kąt 0,19·360° = 68,4°
- fotograf: 3200:29200 ≈ 0,1096, czyli ok. 11%, co daje kąt 0,11·360° = 39,6°
- inne: 2500:29200 ≈ 0,0856, czyli ok. 9%, co daje kąt 0,09·360° = 32,4°
Diagram kołowy:

Wnioski:
Największy udział w koszcie imprezy (ponad 1/3) ma catering. Przygotowując poczęstunek samemu, można istotnie zwiększyć zyski firmy eventowej lub znacznie obniżyć koszt imprezy. Niemal 1/3 kosztów stanowi wynajęcie sali, ale przy balu na 50 par jest to wydatek niezbędny. Można obniżyć koszt poszukując sali w tańszym miejscu (remiza, szkoła). Wynajęcie cateringu, sali i DJ'a to niemal 5/6 wydatków, jednak tylko w pierwszej z tych pozycji można szukać oszczędności nie zmniejszając istotnie standardu usługi. Mniej istotne wydatki połączono w jedną grupę "inne", aby uniknąć wielu drobnych wycinków koła na diagramie.
Zastosowanie w szkole:
- rachunki na liczbach całkowitych, ułamkach i procentach,
- mierzenie kątów płaskich,
- proporcjonalność pól,
- zbieranie, analiza, wizualizacja danych, prowadzenie wnioskowań statystycznych,
- integracja nauczania matematyki z innymi dyscyplinami (historia, geografia, przyroda, ekonomia),
- wprowadzenie na lekcjach różnych przedmiotów elementów statystyki,
- wprowadzenie na lekcjach matematyki elementów historii statystyki,
- tworzenie infografik na potrzeby projektów i codziennego życia szkolnego,
- wykorzystanie arkusza kalkulacyjnego do automatycznego przygotowania diagramu.
Diagramy kołowe w tym artykule wykonano w arkuszu kalkulacyjnym MS Excel. Warto jednak podkreślić, że początkowo wykonywanie diagramów na papierze za pomocą cyrkla, kątomierza i kredek ma znaczne walory kształcące i poznawcze, pozwala też lepiej zrozumieć istotę diagramu kołowego. Kiedy jest on wykonywany automatycznie pomijany jest etap obliczeń i projektowania wyglądu diagramu.
Opinie zasłyszane:
- Jedyną rzeczą gorszą od wykresu kołowego jest wiele wykresów kołowych.
Edward Tufte - amerykański statystyk, pionier w dziedzinie wizualizacji danych
Źródła:
- E. Baranowska, P. Biecek, P. Sobczyk, Wykresy unplugged, Wydawnictwo Uniwersytetu Warszawskiego, Warszawa 2018
- https://en.wikipedia.org/wiki/William_Playfair
- https://www.edwardtufte.com/tufte/
- https://en.wikipedia.org/wiki/Edward_Tufte