Lekcje dotyczące twierdzenia Talesa oraz proporcji trygonometrycznych w trójkącie wielu nauczycieli tradycyjnie przeprowadza w terenie. Jednak są one znacznie ciekawsze, jeśli wykorzysta się na nich prosty, szkolny teodolit. Jest to przyrząd umożliwiający precyzyjny pomiar kątów zarówno w pionie, jak i w poziomie. Do zajęć przyda się także dalmierz lub zwykła taśma miernicza.


Po zapoznaniu ze sprzętem, sposobem jego wyskalowania i zasadami obsługi, klasa podzielona na mniejsze grupy przystąpiła do rozwiązywania zadań.
Zadania dla uczniów
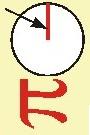
- Wyznacz aktualny kąt wzniesienia Słońca. Pamiętaj, żeby nie patrzeć bezpośrednio w tarczę słoneczną. Użyj okularów ochronnych.
- Wyznacz pozorną średnicę tarczy Słońca w zenicie i oblicz jej rzeczywistą długość. Jaka wielkość fizyczna będzie do tego potrzebna?
- Wyznacz wysokość budynku gospodarczego, znajdującego się na szkolnym podwórku.
- Oblicz powierzchnię szkolnego boiska do piłki nożnej.
- Wyznacz wysokość najwyższego drzewa, które rośnie na terenie należącym do szkoły.
- Oszacuj objętość drewna zawartego w pniu tego drzewa.
- Za pomocą pomiarów i rachunków wyznacz wzrost swojego kolegi z grupy i porównaj go z wynikiem dokładnym. Jaki procentowy błąd popełniłeś?






Szkice rozwiązań
1.
Uwagi
Pomiary i obliczenia na boisku zajęły uczniom około godziny lekcyjnej. Później w klasie sprawdzaliśmy i porównywaliśmy wyniki. Okazało się, że największe problemy sprawiła im nie matematyka i obliczenia, ale zamiana jednostek i techniczna obsługa przyrządów (w tym taśmy mierniczej). Ostatecznie wyniki we wszystkich grupach wyszły w miarę zbliżone. Największe rozbieżności wystąpiły przy pomiarze wysokości drzewa.