Tesselacje

Autor:

Ewa Karolczak

grafik komputerowy

Tesselacja oznacza regularny podział płaszczyzny na "komórki". W języku polskim częściej używamy słowa "parkietaż". Łacińskie słowo „tessela” oznacza małą kwadratową płytkę, których używano w starożytnym Rzymie do układania mozaik.

Najbardziej regularne tesselacje nazywamy (w analogii do wielościanów):

platońskimi (lub foremnymi), gdy składają się z jednego rodzaju wielokątów foremnych (trójkątów, kwadratów lub sześciokątów),
archimedesowymi (lub półforemnymi), gdy składają się z różnych wielokątów foremnych, które tworzą przystające układy w wierzchołkach.

Istnieją też mniej regularne parkietaże (johnsonowskie, rombowe, aperiodyczne i inne), ale nimi nie będziemy się tutaj zajmowali.

Tesselację w technice origami wprowadził Shuzo Fujimoto - japoński nauczyciel chemii, autor książki „Solid Origami” (1976). Jednym z najbardziej znanych artystów stosujących obecnie tę technikę jest Amerykanin - Eric Gjerde. Zapraszamy do odwiedzenia jego strony internetowej.

Galerię tesselacji wykonanych w technice origami można obejrzeć tutaj.

Proponujemy zapoznanie się ze sposobem wykonania najprostszych tesselacji na bazie sieci kwadratowej.

Legenda

1. Model dla początkujących

Zaczniemy od wykonania pojedynczego elementu tesselacji. Na kwadratowej kartce zaginamy siatkę 16 kwadratów w układzie 4×4, jak pokazano na rysunkach 1-5.

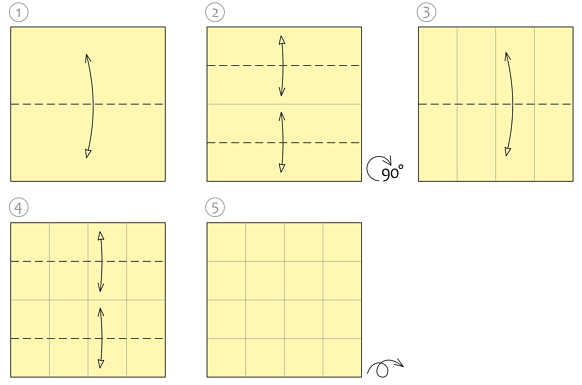
W kolejnym kroku zaginamy jeden narożnik. Aby ułatwić sobie zadanie, należy mocniej zagiąć dwie linie wskazane na rys. 6 i postępować zgodnie z diagramem pokazanym na rys. 7, dbając o wykonanie ostrych zagięć. Gotowy efekt przedstawia rys. 8. W ten sam sposób postępujemy z pozostałymi narożnikami. Przy zaginaniu kolejnych, te które są już zrobione, mogą się otwierać, ale dzięki mocnym zagięciom bardzo łatwo je ponownie złożyć.

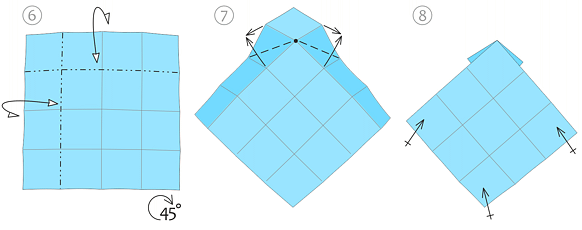
Po zagięciu czterech wierzchołków model wygląda tak jak na rysunkach 9 i 10 (widok z obu stron). Ta forma nosi nazwę modułu Fröbela. Następnie na wewnętrznej stronie tego modułu zaginamy trójkątne skrzydełka (rys. 10-11), a potem po odwróceniu modelu w jego narożnikach formujemy „poduszeczki” jak na rys, 12-15.

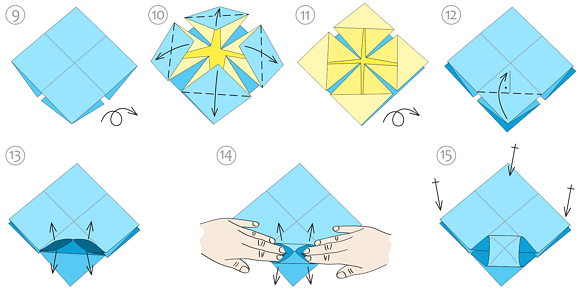
Poniżej przedstawiamy końcowy efekt wykonanych operacji (widok z obu stron). Z kartki o wymiarach 14 cm × 14 cm otrzymamy model wielkości 7 cm × 7 cm.

Przyglądając się raz jeszcze modułowi Fröbela z rys. 9, widzimy, że po wyprostowaniu papieru zagięcia znajdują się tylko na kwadratach leżących na obwodzie kartki. Środkowa część modułu (zaznaczona na czerwono) pozostaje płaska, bez konstrukcyjnych zagięć.

2. Model dla średniozaawansowanych

Bierzemy teraz większą kartkę, np. 21 cm × 21 cm. Musimy uzyskać na niej siatkę kwadratów w układzie 16×16. Można to zrobić w sposób pokazany poniżej. Zaczynamy jak poprzednio od siatki 4×4.

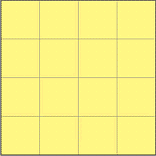
Następnie zagęszczamy ją, dokładając po jednym zagięciu pomiędzy już istniejącymi.

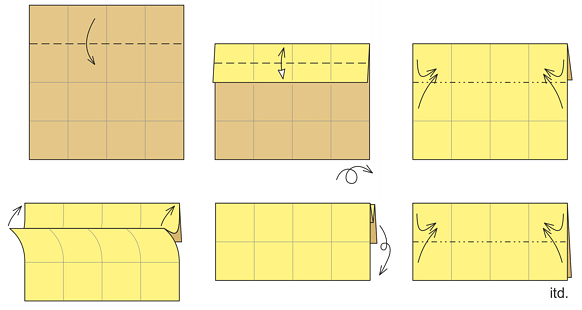
W ten sposób otrzymujemy siatkę 8×8.

Powtarzamy tę czynność jeszcze raz, aby uzyskać siatkę 16×16. Powyższa metoda zaginania sprawia, że kartka jest zagięta w "harmonijkę". Trzeba ujednolicić zagięcia, przeginając je "na zewnątrz".

Na tak przygotowanej kartce znajdujemy kwadraty, które pozostaną do końca płaskie, a zagięcia będziemy wykonywali na ich obwodach. Dla ułatwienia wierzchołki tych kwadratów można lekko zaznaczyć ołówkiem.

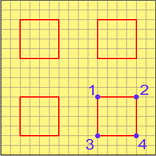
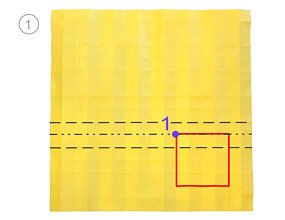
Zacznijmy od wierzchołka nr 1. Wykorzystujemy istniejącą siątkę zagięć i poprawiamy linie tak, aby boki wychodzące z wierzchołka 1 leżały na wypukłych pryzmach (rys. 1-3).

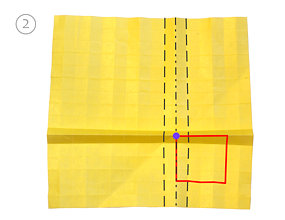
Teraz zaginamy wierzchołek (rys. 4-5) i dociskamy mocno wszystkie zagięcia (rys. 6).

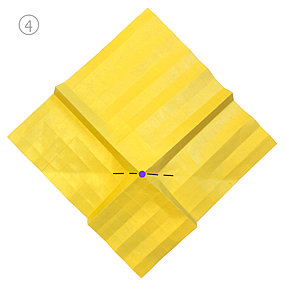
Tak powinno to wyglądać po obu stronach.

Przechodzimy do wierzchołka nr 2. Zaczynamy od uwypuklenia linii łączącej wierzchołki 2 i 4 (rys. 8-9).

Zaginamy wierzchołek 2. Przy tej operacji trzeba nieco rozprostować kartkę przy wierzchołku 1, co powoduje, że poprzednie zagięcie może się trochę otworzyć, ale bardzo łatwo będzie je ponownie złożyć.

Otrzymujemy efekt jak na rys. 12-13 (widok z obu stron).

Analogicznie zaginamy wierzchołek nr 3 (powtarzamy kroki z rys. 8-11). Efekt końcowy po zagięciu trzech wierzchołków przedstawiają rys. 14-15 (widok z obu stron).

Pozostał do zagięcia wierzchołek nr 4.

W tym momencie pierwszy kwadrat tesselacji jest gotowy. Powtarzając powyższe czynności, składamy drugi kwadrat (efekt końcowy widoczny na rys. 20-21).

A potem kolejne dwa (rys. 21-22 wykonane są w powiększeniu w stosunku do poprzednich).

Teraz pozostaje już tylko ukształtowanie "poduszeczek" (jak na rys. 12-15, model I). Końcowy efekt przedstawiono poniżej.

3. Model dla średniozaawansowanych - inaczej

Powyższy model można również wykonać w inny sposób, wykorzystując siatkę zagięć. W tym celu należy najpierw przygotować wszystkie potrzebne zagięcia. Powinny być wykonane dokładnie i mocno dociśnięte, tak by krawędzie były dobrze widoczne. Tak pozaginana kartka staje się na tyle plastyczna, że stosunkowo łatwo uformować z niej wybrany model.

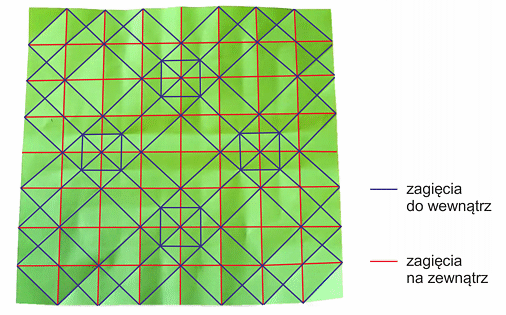
Poniższe film pokazuje krok po kroku, jak wykonać poprzednią tesselację, korzystając z siatki zagięć.

4. Model dla wytrwałych

Po nabyciu umiejętności z modelu I i nabyciu wprawy w modelu II, do kolejnego modelu potrzeba już "tylko" odpowiednio dużo czasu, cierpliwości i motywacji. Na kartce (kwadratowej lub prostokątnej) dowolnej wielkości zaginamy sieć kwadratów i zgodnie z instrukcją przedstawioną powyżej zaginamy kolejne moduły tesselacji. Ewentualne paski zbędnych kwadratów pozostałe na brzegach można odciąć. Dla kartki kwadratowej najlepiej wykonać siatkę n²×n².

Model pokazany na poniższym zdjęciu powstał na bazie siatki 26×26 (na tesselację potrzeba 25×25 i po jednym kwadraciku zostaje na wykończenie brzegów). Pojedynczy kwadrat sieci miał ok. 6,5 mm × 6,5 mm. A tak wygląda gotowy model z obu stron.

Poniżej model wykonany z dwukolorowego papieru na bazie siatki 32×32 .

autor: Aleksandra Heluszka

Poniżej zamieszczamy zdjęcia tesselacji (głównie na sieci trójkątów równobocznych) wykonanych przez uczestników konkursu matematycznego origami "Żuraw".