Równania miłości

Czy miłość da się opisać równaniem matematycznym? Sama miłość - zapewne nie, ale jej odwieczny symbol - serce - a raczej jego geometryczny kształt - jak najbardziej. Zrobimy to na kilka sposobów. Opiszemy serca analitycznie i geometrycznie, a także łamigłówkowo, origamicznie, wyszywankowo i fraktalnie.

Kardioida, czyli krzywa sercokształtna

Rozpocznijmy od klasyki - słynnej krzywej nazywanej kardioidą pisaliśmy już o niej tutaj). Jest ona zakreślana przez ustalony punkt okręgu toczącego się bez poślizgu na zewnątrz po innym, nieruchomym okręgu o tej samej średnicy. Jej własności po raz pierwszy zbadał i opisał duński matematyk i astronom Ole Rømer w 1674 roku. 

Krzywą tę można opisać za pomocą równania kartezjańskiego następująco: (x²+y²–kx)² = k²(x²+y²), gdzie k jest średnicą koła użytego do konstrukcji. Poniższy rysunek przedstawia kardioidę dla k=2.

Serca analityczne

Zachęcamy do poszukiwania jeszcze innych linii, które dobrze imitują kształt serca, oraz ich równań w układzie kartezjańskim. Oto kilka przykładów, które powinny Was zainspirować.

Na początek wykorzystamy dobrze znany wykres funkcji sinus, funkcji do niej odwrotnej, oraz wykresy półokręgów.

Tak wygląda wykres funkcji sinus na przedziałach [0, π/2] oraz [-π/2, π/2].

A tak wykres funkcji odwrotnej - arcus sinus - na przedziałach [0, 1] oraz [-1, 1]

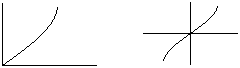
Przesuwając i odbijając odpowiednio te wykresy, można otrzymać podstawy serc.

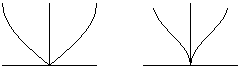
y = arcsin|x|         y = arcsin|x–1| + π/2

Zadanie 1. Podaj wzory funkcji opisujące półokręgi potrzebne do dokończenia tych rysunków.

A teraz jeszcze kilka innych pomysłów na krzywe sercowate.

Zadanie 2. Czy potrafisz dopasować równania do rysunków?

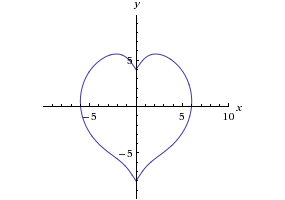
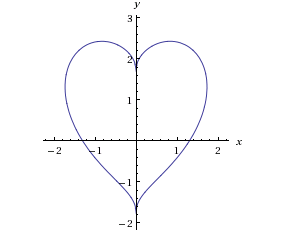
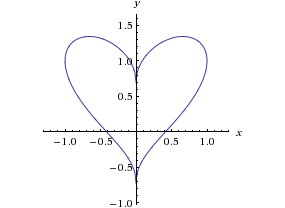
• (x²+y²–1)³ = x²y³
• x²+(y – ²/₃(x²+|x|–6)/(x²+|x|+2))² = 36
• x²+(y–√|x|)_² = 3
• x²+2(y–|x|+0,6)² = 1
• x²+2(y–0,5√|x|)_² = 1
• x²+2(y–√|x|)_² = 1

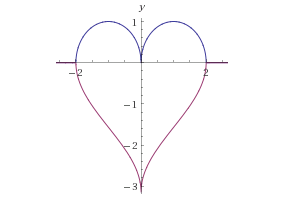
Do wykreślenia jednego serca można też użyć równań dwóch funkcji, jak w poniższych przykładach.

y = √|x| + √(1–x2) y = √|x| – √(1–x2)	y = √(1–(|x|–1)2) y = arccos(1–|x|) – π

Ciekawym sposobem uzyskania kształtu serca jest też połączenie dwóch elips.

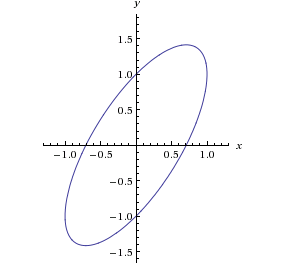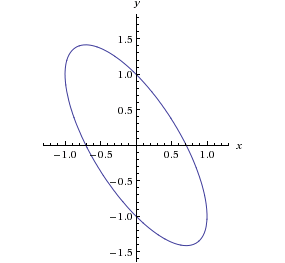2x2–2xy+y2 = 1	2x2+2xy+y2 = 1

Umieszczamy te wykresy w jednym układzie współrzędnych i usuwamy zbędne połówki.

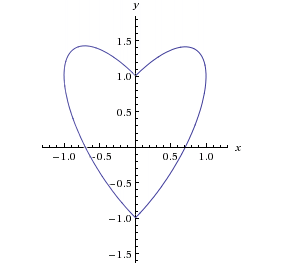
                                                        2x²–2xy+y² = 1   dla x ≥ 0
                                                        2x²+2xy+y² = 1   dla x ≤ 0

Do rysowania walentynkowych serc można też wykorzystać funkcje dwóch zmiennych, których wykresy powstają w trójwymiarowym układzie współrzędnych, np. taki:

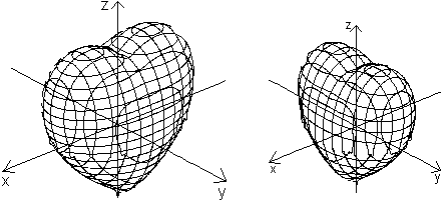
(x² + ⁹/₄y² + z² – 1)³ = x²z³ + ⁹/₈₀y²z³

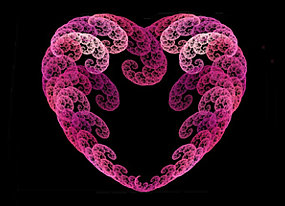
Serca fraktalne

Na pewno każdy z Was słyszał coś fraktalach. Są to obiekty uzyskiwane przez wielokrotne powtarzanie nakładania operacji podobieństwa o ułamkowej skali początkowo na jakąś prostą figurę geometryczna, potem na jej obraz itd w nieskończoność. W efekcie powstaje obiekt samopodobny, którego dowolna część jest zawsze podobna do całości. Fraktale także opisuje się równaniami funkcji, ale najczęściej wykorzystuje się do tego liczby i funkcje zespolone. Oczywiście można je potem wykorzystać do tworzenia matematycznych serc. Poniżej kilka przykładów. Pierwszy z nich nazywany jest zbiorem Mandelbrota. Wyraźnie można w nim zauważyć naszą dobrą znajomą - kardioidę.

Serca geometryczne

Do szkicowania wykresów funkcji przypominających serce używaliśmy komputera, ale matematyczne serca można otrzymać także metodami klasycznymi, konstruując je cyrklem i linijką.

Zadanie 3. Czy potrafisz odtworzyć poniższe konstrukcje?

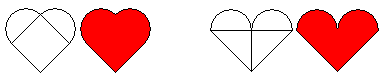
Te serca powstały z kwadratu i koła.

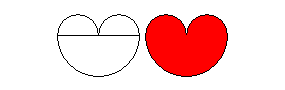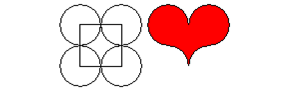To powstało z dwóch różnych kół.	A to - z kwadratu i czterech kół.

To serce powstało z deltoidu i koła.	A to - z dwóch kół oraz stycznych.

Więcej zadań o geometrycznych sercach znajdziesz w artykułach Serca i łuki (1) oraz Serca i łuki (2).

Na koniec wróćmy jeszcze raz do kardioidy. Okazuje się, że można ją wykreślić za pomocą samego cyrkla! Ten, jak wiadomo, służy do kreślenia okręgów, ale kardioida jest obwiednią rodziny okręgów, których środki leżą na ustalonym okręgu i które przechodzą wszystkie przez jeden punkt tego okręgu. Własność tę pokazuje poniższy rysunek (czerwone punkty to środki wybranych okręgów z prezentowanej rodziny, a żółty to punkt wspólny wszystkich okręgów). Chociaż na rysunku wykreślone są wyłącznie okręgi, wyraźnie widać na nim kształt kardioidy.

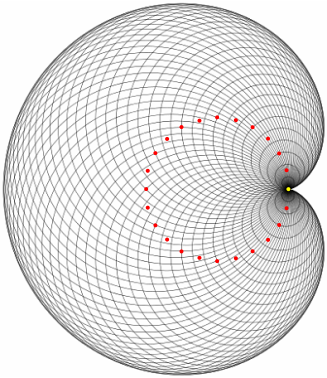
Serce - tangram

Klasyczna chińska łamigłówka o nazwie tangram występuje także w odmianie "serce". Bardzo łatwo można ją wykonać z kartonu samodzielnie na podstawie poniższego rysunku i sprezentować w formie łamigłówkowej walentynki.

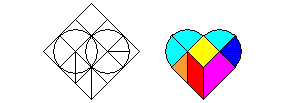
Serce - origami

A oto instrukcja wykonania walentynki w kształcie serca z papieru.

Serce - wyszywanka

Po raz kolejny wracamy do kardioidy. Ma ona jeszcze jedną ciekawą własność opisaną w 1996 roku przez dwójkę amerykańskich matematyków - Dinę Rojas i Michaela McDonalda. Rozważmy 40 punktów (ponumerowanych od 0 do 39) rozłożonych równomiernie na okręgu. Teraz łączmy punkt o numerze n z punktem o numerze będącym resztą z dzielenia liczby 2n przez 40. Powstałe linie stanowią obwiednię pewnej kardioidy, tzn. są do niej styczne. Własność tę można wykorzystać do wykonania własnoręcznej walentynki w wersji wyszywanej.

Widzicie zatem, jak wiele można mieć pomysłów na serca opisane matematycznym równaniem lub geometryczną konstrukcją. Mam nadzieję, że dzięki eksperymentom z funkcjami i figurami stworzycie wiele nowych ciekawych serc i niepowtarzalnych walentynek dla swoich sympatii lub nauczycieli matematyki. A niepoprawnym matematycznym romentykom polecamy również lekturę artykułu Alfabet miłości.