Nagroda Forda dla wrocławskich matematyków

W sierpniu 2010 roku w Pitsburgu podczas dorocznego zebrania członków Amerykańskiego Stowarzyszenia Matematycznego (zrzeszającego oprócz zawodowych matematyków także, a może przede wszystkim, nauczycieli i miłośników matematyki) nagrodę im. Lestera Forda za najlepszy artykuł w roku akademickim 2009/2010 opublikowany w czasopiśmie "The American Mathematical Monthly" odebrało dwóch wrocławskich matematyków: Jerzy Kocik (obecnie Southern Illinois University, USA) i Andrzej Solecki (obecnie Universidade Federal we Florianopolis, Brazylia). Nagrodzony artykuł zawiera elementarne, geometryczne (można nawet powiedzieć "obrazkowe") dowody tożsamości trygonometrycznych i innych twierdzeń z geometrii trójkąta.

Nagroda Lestera R. Forda została ustanowiona w 1964 roku i co roku jest wręczana autorom najciekawszych artykułów publikowanych na łamach czasopisma "The American Mathematical Monthly". Początkowo nagrody te były wręczane za publikacje w "The American Mathematical Monthly" lub w "Mathematics Magazine", ale od 1976 roku za najlepsze publikacje w tym drugim piśmie ustanowiono nagrody Carla B. Allendoerfera i od tej pory nagrody Forda przyznawane są tylko za teksty w "Monthly". Co roku tą nagrodą w wysokości 500 dolarów wyróżnianych jest do pięciu artykułów. Ogłoszenie laureatów i wręczenie nagród ma miejsce na dorocznych letnich spotkaniach MAA (Mathematical Association of America). Większość nagrodzonych do tej pory teksów można znaleźć tutaj.

Nazwa nagrody upamiętnia Lestera R. Forda Seniora, znakomitego matematyka, redaktora naczelnego "The American Mathematical Monthly" w latach 1942–1946 oraz prezesa Amerykańskiego Stowarzyszenia Matematycznego w latach 1947–1948.

Artykuł Jerzego Kocika i Andrzeja Soleckiego p.t. "Disentangling a Triangle" (rozmontowując trójkąt), który ukazał sie w numerze marcowym 2009 (vol. 116, no. 3, March 2009, pp. 228-237), to prawdziwy dydaktyczny majstersztyk. Wyróżniono go ze względu na wyjątkowe (geometryczne!) spojrzenie autorów na trygonometrię. Zawiera on wiele elementarnych twierdzeń z geometrii trójkąta, które wykorzystane są do prostego i eleganckiego uzasadnienia tożsamości trygonometrycznych oraz twierdzenia o okręgu dziewięciu punktów. Wszystko sprowadza się do serii przejrzystych rysunków zamiast długich rachunków algebraicznych. Jest to oryginalne podsumowanie wiedzy na temat funkcji trygonometrycznych wykorzystujące ich geometryczne interpretacje. Okazuje się, że z geometrycznych interpretacji sinusa i kosinusa można odczytać wiele trygonometrycznych zależności. Stoi za tym geometria, nie rachunki. Trygonometrię można więc (i trzeba) widzieć. Niestety, jak pisze jeden z autorów nagrodzonego artykułu: nastawienie na wymuszoną algebraizację geometrii przeważyło i wymordowało geometrię w szkołach, z tragicznymi dla pojmowania matematyki skutkami.

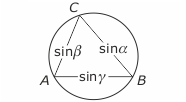Rysunek obok pokazuje geometryczną interpretację twierdzenia sinusów dla trójkąta wpisanego w okrąg o średnicy 1. Sinusy kątów są wtedy długościami boków tego trójkąta.

Istotę geometrii trójkąta autorzy upatrują we własnościach
ortocentrycznej czwórki punktów i jej poświęcają osobno sporo uwagi pod
koniec artykułu, wprowadzając nowatorski sposób zapisu, pozwalający łatwo sformułować i uogólnić odkryte wcześniej własności. Na końcu zamieszczają też listę ciekawych zadań do samodzielnego rozwiązania, pozostawiając tym samym wiele frajdy czytelnikom. 

Obaj autorzy są związani z Uniwerystetem Wrocławskim. Andrzej Solecki studiował tu matematykę (gdyż uznał ją za dyscyplinę, która nie zależy od geopolityki, jej opanowanie nie zabiera dużo czasu, można się nią dobrze bawić i uprawiać ją samotnie - czas pokazał, że miał tylko 50% racji), a Jerzy Kocik - fizykę teoretyczną, którą jednak porzucił dla matematyki (twierdząc, że ta kreuje wiele rzeczywistości, podczas gdy fizyka tylko jedną) i obecnie zajmuje się głównie algebrami Liego i geometrią różniczkową.

Nagrodzony artykuł można przeczytać tutaj. Natomiast tutaj można znaleźć komentarz Andrzeja Soleckiego do tego artykułu, zaczynający się od słów: Dobra nowina dla wszystkich ofiar długich i nudnych przekształceń algebraicznych, nazywanych sadystycznie „tożsamościami trygonometrycznymi”. Otóż wykończyliśmy tę nudę celnym strzałem srebrną kulą i na wszelki wypadek pokryliśmy resztki tych flaków z olejem grubą warstwą czosnku. Bez czyjejś pomocy ta zmora nie podniesie się więcej.