Kopalnia metod

Trójkąt równoboczny ABC wpisano w okrąg, a następnie na łuku BC obrano dowolny punkt M. Okazuje się, że |MA| = |MB| + |MC|. Ten zaskakujący fakt wykażemy na kilkanaście sposobów. Niektóre dodwody opierają się na podobnym pomyśle, więc będą prezentowane pod wspólnym tytułem.

Metoda "prowadzenia prostej równoległej"

Dowód 1. Poprowadźmy cięciwę CD równoległą do MB i niech przetnie ona odcinek AM w punkcie F. Oczywista jest równość długości odcinków CM i DB, a tym samym równość miar kątów CAM i DAB. Otrzymujemy zatem |∡DAM| = |∡DAB|+|∡MAB| = |∡MAB|+|∡CAM| = 60°. Z drugiej strony |∡ADC| = |∡ABC| = 60°. Oznacza to, że trójkąt ADF jest równoboczny. Dalej mamy |∡CFM| = |∡AFD| = 60° i |∡CMF| = |∡CBA| = 60°, więc trójkąt CFM też jest równoboczny. Z równości miar kątów ACD i BCM będących róznicą tych samych kątów mamy |AD| = |MB|. Ostatecznie |AM| = |AF| + |FM| = |MB| + |MC|.

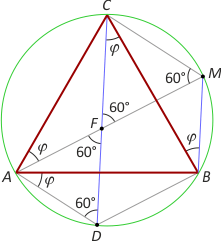
Dowód 2. Można poprowadzić prostą BD równoległą do AM i przeprowadzić analogiczne rozumowanie.

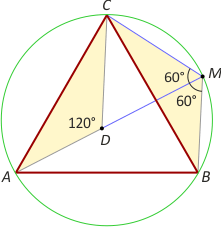
Metoda "odkładania odcinków"

Dowód 3. Na odcinku AM odłóżmy odcinek DM przystający do MC. Wówczas trójkąt równoramienny CDM jest równoboczny, bo |∡CMD| = |∡CBA| = 60°. Rozważmy teraz trójkąty ADC i CMB. Mamy |∡CMB| = |∡CMA|+|∡AMB| = 60°+60° = 120° oraz |∡ADC|=120° (bo to kąt przyległy do kąta CDM). Dalej |AC|=|BC| oraz |CD|=|CM|, a stąd na mocy cechy bkb trójkąty ADC i CMB są przystające i |AD|=|MB|. Ostatecznie |AM| = |AD|+|DM| = |MC|+|MB|.

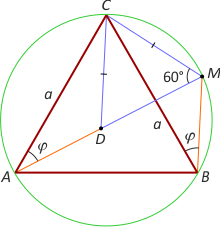
Dowód 4. Na odcinku AM odłóżmy odcinek AD przystający do MB. Wówczas trójkąty ADC i BMC są przystające z cechy bkb, bo |∡CAD| = |∡CBM|, |AD|=|MB| i |AC|=|BC|, zatem |CD|=|MC|. Dalej |∡CMD| = |∡CBA| = 60°, co oznacza, że trójkąt równoramienny CDM jest równoboczny i |DM|=|CM|. Ostatecznie |AM| = |AD|+|DM| = |MC|+|MB|.

Metoda "przedłużania i odkładania odcinków"

Dowód 5. Na przedłużeniu BM odłóżmy odcinek MN przystający do MC. Zauważmy, że |∡CMN| = 60°, bo jest to kąt zewnętrzny dla czworokąta ABMC. Stąd trójkąt CMN jest równoboczny. Dalej mamy |AC|=|BC|, |CM|=|CN| i |∡ACM| = 60°+|∡BCM| = |∡BCN|, stąd na mocy cechy bkb trójkąty AMC i BCN są przystające i |AM|=|BN|. Mamy zatem |AM| = |BN| = |MB|+|MN| = |MB|+|MC|.

Dowód 6. Na przedłużeniu BM poza punkt B odkładamy odcinek BN przystający do MC. Mamy wówczas |∡ACM| = |∡ABN| i na mocy cechy bkb trójkąty ACM i ABN są przystające, przy czym |AM|=|AN|. Dalej |∡AMB| = |∡ACB| = 60°, zatem trójkąt AMN jest równoboczny. Ostatecznie |AM| = |MN| = |MB|+|BN| = |MB|+|MC|.

Dowód 7.  Na odcinku AM odkładamy odcinek DM przystający do MC. Przedłużamy CD do przecięcia w punkcie E z okręgiem opisanym na trójkącie i łączymy punkt E z wierzchołkiem A. Trójkąt CDM jest równoboczny (patrz dowód 3). Zauważmy, że |∡ACM| = 60°+|∡BCM| = 60°+|∡ACE|, a stąd |∡BCM| = |∡ACE| i |AE|=|MB|. Łatwo zauważyc, że trójkąt AED też jest równoboczny. Mamy zatem |AM| = |AD|+|DM| = |AE|+|DM| = |MB|+|MC|.

Dowód 8.  Na przedłużeniu MB poza punkt B odkładamy odcinek ME przystający do MA. Ponieważ |∡AMB| = 60°, trójkat równoramienny AME jest równoboczny. Prowadzimy odcinek BD równoległy do AE. Łatwo zauważyć, że czworokąt AEBD jest równoległobokiem i |AD|=|BE|. Dalej mamy |∡ABD|+|∡DBC| = 60° = |∡DBC|+|∡CBM|, a stąd |∡ABD| = |∡CBM| i |AD|=|MC|. Ostatecznie |AM| = |ME| = |MB|+|BE| = |MB|+|AD| = |MB|+|MC|.

Metody "narzędziowe" 

Dowód 9. Z twierdzenia kosinusów. Oznaczmy |AM|=x, |MB|=y i |MC|=z. W trójkątach  ABM i CBM z twierdzenia kosinusów zachodzi a² = x²+y²–xy oraz a² = z²+y²+zy, skąd otrzymujemy równanie x²+y²–xy–z²–y²–zy = 0 i po przekształceniach mamy (x+z)(x–y–z) = 0. Stąd x = y+z, czyli |AM| = |MB|+|MC|.

Dowód 10. Z twierdzenia sinusów. W trójkątach ABM i AMC z twierdzenia sinusów zachodzi |MB| = 2Rsinφ, |MC| = 2Rsin(60°–φ) oraz |AM| = 2Rsin(60°+φ). Podstawiając do równości |AM| = |MB|+|MC|, mamy 2Rsin(60°+φ) = 2Rsin(60°–φ) + 2Rsinφ. Po zastosowaniu wzorów trygonometrycznych otrzymujemy tożsamość 0=0, c.k.d.

Dowód 11. Przez sumowanie pól. Zauważmy, że P_ABMC = P_ABM + P_AMC. Niech |∡CAM| = |∡CBM| = α oraz |∡AKB| = φ. Mamy wówczas φ = 60°+α, bo φ jest kątem zewnętrznym w trójkącie AKC. Dalej |∡ABM| = 60°+α = φ. Z kolei |∡ACM| =180°–|∡ABM| = 180°–φ. Wracając do wyjściowego równania, otrzymujemy ¹/₂|AM|·a·sinφ = ¹/₂|MB|·a·sinφ + ¹/₂|MC|·a·sin(180°–φ), skąd po zastosowaniu wzoru redukcyjnego i podzieleniu obu stron równania przez ¹/₂·a·sinφ otrzymujemy tezę.

Dowód 12. Z twierdzenia Ptolemeusza. Z twierdzenia Ptolemeusza otrzymujemy |AM|·a = |MB|·a + |MC|·a skąd po podzieleniu obu stron równości przez a mamy tezę.

Dowód 13. Przez obracanie. Na odcinku AM odkładamy odcinek DM przystający do MB. Trójkąt BMD jest równoboczny. Obracamy trójkat BMC o 60° wokół wierzchołka B. Wówczas punkt C przechodzi na wierzchołek A, a punkt M przechodzi na D. Trójkąty ADB i BMC są przystające z cechy bkb, bo |DB|=|MB|, |AB|=|BC| i |∡ADB| = |∡BMC| = 120°. Zatem |AD|=|MC| i ostatecznie |AM| = |AD|+|DM| = |MB|+|MC|.

Dowód 14. Ze wzoru na dwusieczną. Długość dwusiecznej kąta A o mierze α w trójkącie ABC wynosi l_a = ^2bc/_(b+c)·cos(^α/₂).  Zauważmy, że ML jest dwusieczną kąta CMB. Stosując powyższy wzór, mamy (*) |ML| = ^|MC|·|MB|/_(|MC|+|MB|). Z drugiej strony trójkąty ACM i MLB są podobne z cechy kkk (wspólne są kąty φ i 60°). Stąd mamy proporcję |MA|:|MC| = |MB|:|ML|. Po podstawieniu za |ML| do (*) otrzymujemy tezę. 

Można by tak kontynuować dowodzenie w nieskończoność... Z pewnością miłośnicy geometrii pomogą ten zestaw dowodów uzupełnić jeszcze o conajmniej 10 innych (przynajmniej tyle zna jeszcze autor tekstu). Zapraszamy do wpisywania ich w komentarzach.