|
Wydaje się, że wykres funkcji
a) mieści się pod parabolą
b) ma 'górki' (maksima) w punktach styczności z tą parabolą
Uzasadnij, że NIE.
c) ma 'dołki' (minima) w punktach styczności z osią OX
Uzasadnij, że TAK.
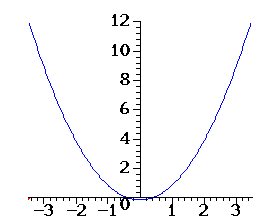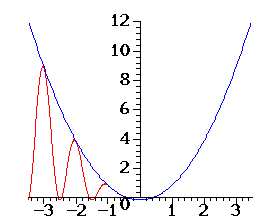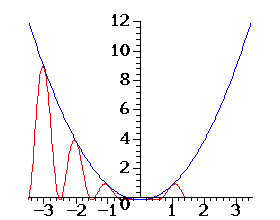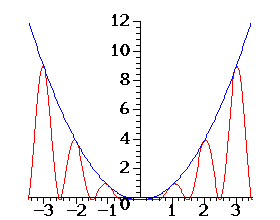
d) ma maksima dla argumentów całkowitych
Uzasadnij, że NIE.
e) ma minima dla argumentów postaci k+0,5, gdzie k - całkowite
Uzasadnij, że TAK.
UWAGA! Uzasadnij powyższe fakty BEZ liczenia pochodnej.
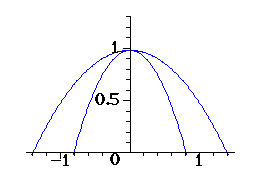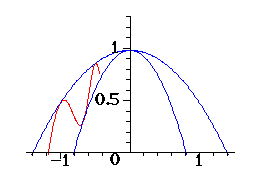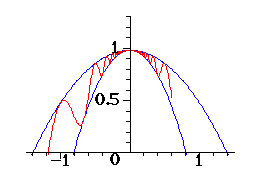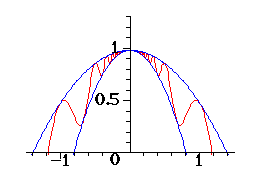
|
A co się wydaje, gdy patrzymy na wykres tej funkcji?
Co z powyższych obserwacji jest prawdą, a co się tylko wydaje?
Jak wygląda ten wykres 'z daleka' ?
Wskazówka: Sprawdź, że $g\left(\frac{1}{n}\right) - g\left(\frac{1}{n+1{/}4}\right) > 0$. Co to oznacza?



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


