KĄCIK NAUKOWY › Kółko matematyczne

W labiryncie

Data ostatniej modyfikacji:
2010-08-10
Autor: 
Piotr Kryszkiewicz
nauczyciel w ZS w Miliczu
Poziom edukacyjny: 
szkoła podstawowa
gimnazjum
szkoła średnia z maturą
szkoła profilowana zawodowa
Dział matematyki: 
łamigłówki logiczne

Wśród łamigłówek logicznych często pojawiają się rozmaite zadania labiryntowe. Nie wymagają one właściwie żadnej specjalistycznej wiedzy matematycznej, jedynie spostrzegawczości, wyobraźni, czasem biegłości rachunkowej i odrobiny wprawy. Znakomicie nadają się na kółko matematyczne lub zajęcia na zielonej szkole.

Prezentowane tu zadania pochodzą (w większości) z różnych edycji Międzynarodowych Mistrzostw w Grach Matematycznych i Logicznych (więcej zadań z tych zawodów można znaleźć na stronie  http://www.gmil.prv.pl). Ułożone są ze względu na rosnący stopień trudności, co powinno ułatwić ich rozwiązywanie lub wykorzystanie na kółku matematycznym.

Prosimy o dopisywanie w komentarzach kolejnych zadań dotyczących labiryntów (ew. rysunki można wysłać e-mailem na adres redaktora działu "Kółko matematyczne"), zamieszczania linków do takich zadań lub dzielenia się swoimi pomysłami rozwiązań.

 
Zadanie 1. Eliminacje 2002
Na planie Muzeum Precjozów podano liczby eksponatów znajdujących się w poszczególnych salach. Z braku czasu Jaś Wędrowniczek musi ograniczyć zwiedzanie do sześciu sal. Idąc od wejścia do wyjścia wybrał taką trasę, by zobaczyć możliwie najwięcej precjozów. Ile ich obejrzał?

  
Zadanie 2. Eliminacje 2004
Na planie Muzeum Precjozów podano liczby eksponatów znajdujących się w poszczególnych salach. Jaś Wędrowniczek idąc od wejścia do wyjścia nigdy nie znalazł się dwukrotnie w tej samej sali i obejrzał w sumie 13 eksponatów. Iloma trasami mógł zwiedzać muzeum?

  
Zadanie 3. Eliminacje 1996
Na rysunku przedstawiono plan osiedla Kwadratkowo. Każdy kompleks domów jest kwadratem o boku 100 m, a cała osada zajmuje kwadratowy teren o boku 800 m (szerokość ulic zaniedbujemy). Ruch na osiedlu odbywa się tylko ulicami. Jaką najkrótszą drogę trzeba przemierzyć ze skrzyżowania A do B? Ile jest takich dróg?

  
Zadanie 4. Eliminacje 1997
Na rysunku przedstawiono plan osiedla Kwadratkowo. Składa się ono z 48 kwadratowych bloków i ulic tworzących 59 skrzyżowań. Ruch na osiedlu odbywa się tylko ulicami. Julia wyznaczyła Romeo spotkanie na skrzyżowaniu leżącym w jednakowej odległości zarówno od skrzyżowań A i B jak i C i D. Na którym skrzyżowaniu powinien czekać Romeo? Jaka jest szansa, że spotka się z Julią?

  
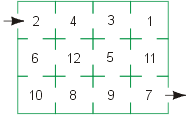
Zadanie 5. Półfinał krajowy 2006
W labiryncie dodaje się liczby z pól, przez które się przechodzi. Nie można przechodzić z jednego pola na drugie, jeżeli nie mają one wspólnego boku oraz nie można przechodzić dwa razy przez to samo pole. Jaką największą sumę można osiągnąć przechodząc przez ten labirynt?

  
Zadanie 6. Finał międzynarodowy 1996
Wchodzisz z zawiązanymi oczami do labiryntu składającego się z 16 pomieszczeń. Po przejściu przez pierwsze drzwi idziesz po omacku wzdłuż ściany po twojej lewej stronie, aż do następnych drzwi. Przechodzisz przez te drzwi i idziesz dalej, ale wzdłuż ściany po twojej prawej stronie, aż dojdziesz do następnych drzwi. Przechodzisz przez te drzwi i znowu idziesz wzdłuż ściany lewej do następnych drzwi itd. Przechodzisz na zmianę wzdłuż ściany prawej i lewej. Podaj kolejność pomieszczeń, przez które przejdziesz od wejścia do labiryntu do jego opuszczenia.

  
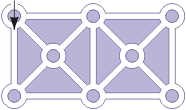
Zadanie 7. Finał międzynarodowy 1995
Wchodzisz z zawiązanymi oczami do labiryntu składającego się z 8 rond i idziesz po omacku w kierunku oznaczonym strzałką. Na pierwszym rondzie skręcasz w pierwszą ulicę w lewo, na drugim – w pierwszą w prawo, potem znowu w pierwszą w lewo itd. Skręcasz na zmianę w lewo i w prawo. Przez ile rond musisz przejść od wejścia do labiryntu do jego opuszczenia?

  
Zadanie 8. Eliminacje 2000
W labiryncie można przechodzić z jednej kratki do bezpośrednio z nią sąsiadującej, tzn. mającej z nią wspólny bok. Jeżeli jesteśmy w kratce z liczbą d, to możemy przejść do kratki leżącej:

  • powyżej, jeśli liczba d jest wielokrotnością 3,
  • poniżej, jeśli liczba d jest wielokrotnością 4,
  • na prawo, jeśli liczba d jest wielokrotnością 5.

Jaka droga prowadzi od wejścia do wyjścia?

  
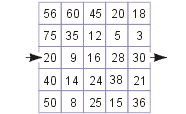
Zadanie 9. Finał międzynarodowy 1996
W labiryncie można przechodzić z jednej kratki do bezpośrednio z nią sąsiadującej, tzn. mającej z nią wspólny bok, ale tylko wtedy, gdy liczby umieszczone w tych dwóch kratkach mają wspólny dzielnik większy od 1. Jaka droga prowadzi od wejścia do wyjścia? Ile jest dróg, w których przez każdą kratkę przechodzi się co najwyżej jeden raz?

  
Zadanie 10. Finał międzynarodowy 2002
Małe Muzeum Precjozów składa się z czterech jednakowych kwadratowych sal o wymiarze 10 m x 10 m. Przepierzenie o długości 10 m (zaznaczone grubą kreską) wystarczy, aby w MMP wyznaczyć trasę od wejścia do wyjścia, która obchodzi wszystkie sale, każdą tylko raz.

Wielkie Muzeum Precjozów ma 16 sal o wymiarach 10 m x 10 m. Dyrektor tego muzeum także chciałby wyznaczyć trasę od wejścia do wyjścia, która przechodzi przez wszystkie sale, przez każdą tylko raz. Ile co najmniej przepierzeń o długości 10 m jest mu do tego potrzebnych? Przepierzenie może być postawione wyłącznie wzdłuż linii przerywanych.

  
Zadanie 11. Półfinał krajowy 1995
Ariadna codziennie patroluje labirynt w skarbcu królewskim od komnaty A do B, układając wzdłuż trasy sznurek. Przez każdy korytarz musi przejść dokładnie raz, a sznurek nie może krzyżować się na żadnym skrzyżowaniu (choć przez dane skrzyżowanie można przechodzić kilkukrotnie). Ariadna zbadała wszystkie możliwe drogi i opracowała plan obchodów tak, aby codziennie patrolować skarbiec inną drogą. Ile dni zajmie jej realizacja tego planu?

  
Zadanie 12. Finał międzynarodowy 1994
Skarbiec w banku Tezaurusa podzielony jest na 36 sal, w których umieszczone są sejfy. Każdej nocy strażnik patroluje skarbiec rozpoczynając i kończąc obchód w sali A. Przez każdą z pozostałych sal musi przejść dokładnie raz. Strażnik zbadał wszystkie możliwe drogi i opracował plan obchodów tak, aby każdej nocy patrolować skarbiec inną drogą. Ile nocy zajmie mu realizacja tego planu?

  
Dwa ostatnie zadania o labiryntach więziennych zostały zaczerpnięte z rewelacyjnej książki Borysa Kordiemskiego Rozrywki matematyczne (Wiedza Powszechna, 1958).
  
Zadanie 13. Sto czterdzieści pięć drzwi
W więziennym labiryncie znajduje się 145 drzwi, z tego 9 jest zamkniętych, a pozostałe są otwarte na oścież. Należy przejść labirynt, otwierając po drodze wszystkie 9 zamkniętych drzwi. Jednak każde z tych drzwi otwierają się pod warunkiem, że wcześniej przeszło się przez 8 otwartych drzwi. Ponadto ostatnie drzwi prowadzące na wolność otworzą się jedynie pod warunkiem, że więzień przejdzie przez wszystkie pomieszczenia, odwiedzając każde dokładnie raz. Jaką trasę musi pokonać, jeśli znajduje się początkowo w celi W?

  
Zadanie 14. Jak więzień wydostał się na wolność?
Więzienie składa się z 49 cel. Drzwi każdej celi są zamknięte i otwierają się przez popchnięcie tylko w jedną stronę (wskazaną na rysunku), a po ich przekroczeniu zamykają się, więc nie można przez nie wrócić. Ponadto drzwi oznaczone wielkimi literami otwierają się jedynie kluczem oznaczonym małą literą. Oznacza to, że drzwi na wolność G otwierają się kluczem g. Więzień znajduje się w celi W. Jaką drogą może wydostać się na wolność? Ile drzwi w sumie przekroczy?

  

 

Powrót na górę strony