KĄCIK NAUKOWY › Kółko matematyczne

Szprychy w cylindrze (1) - f-schody

Data ostatniej modyfikacji:
2012-06-13
Autor: 
Krzysztof Omiljanowski
pracownik IM UWr
Poziom edukacyjny: 
szkoła średnia z maturą
szkoła profilowana zawodowa
Dział matematyki: 
funkcje
geometria przestrzenna
Do rysunków 3D użyto apletu www.javaview.de/
Można nimi manipulować myszą.


 

Poniższe powierzchnie są tworzone według jednakowego schematu.
Najlepiej to widać na czwartym rysunku. Sprawdź.





Każda z tych powierzchni jest utworzona z patyków-odcinków jednakowej długości (=1), doczepionych jednym końcem do wspólnej osi pod kątem prostym.
Cała powierzchnia mieści się w cylindrze o promieniu 1, a patyki są prostopadłe do osi cylindra.
Patrząc z góry, widać, że nad każdą 'szprychą' w podstawie cylindra jest jeden patyk.
Trochę 'żłobiąc' nasze figury, otrzymamy kręte schody, w których patyki są krawędziami stopni.
Przepis na otrzymanie takich powierzchni jest następujący:

dla zadanej funkcji f (x), określonej na odcinku [0,1],
nad 'szprychą' w podstawie, która tworzy z osią OX kąt x . 360o,
zaczepiamy w osi patyk długości 1, na poziomie f (x).
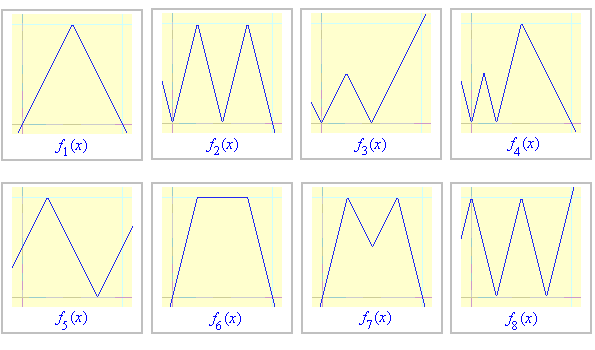
Stąd robocza nazwa rozważanych powierzchni: f-schody.

 

ZADANIE 1. Jak wyglądają f-schody, gdy f jest funkcją o wykresie jak niżej?
Wpisz poniżej wzór wybranej funkcji f i sprawdź, jak wyglądają dla niej f-schody.


Wskazówki 

 

 

 

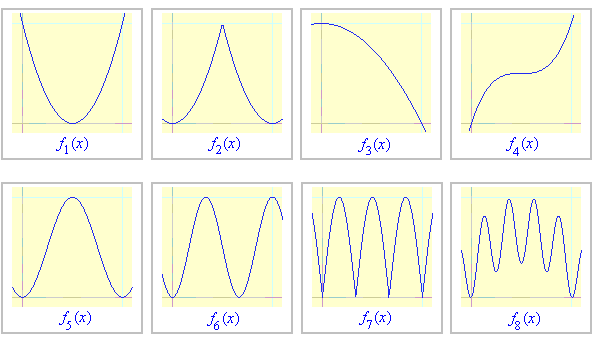
ZADANIE 2. Jak wyglądają f-schody, gdy f jest funkcją o wykresie jak niżej?
Wpisz poniżej wzór wybranej funkcji f i sprawdź, jak wyglądają dla niej f-schody.

 

 

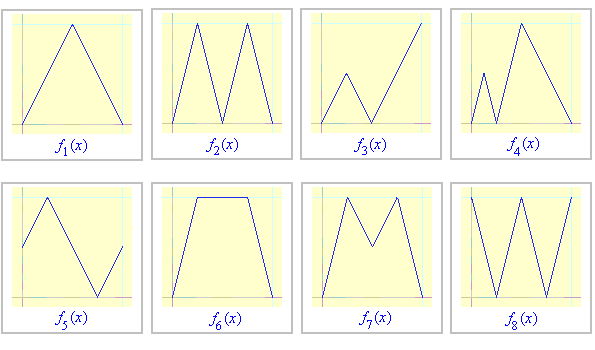
ZADANIE 3.a. Dla których funkcji fk, objętość bryły 'pod schodami' jest równa /2, gdy fk jest funkcją o wykresie jak niżej?
Uwagi
Dla danej funkcji fk bryłę ograniczają: powierzchnia boczna cylindra, podstawa cylindra i powierzchnia fk-schodów.
Dla każdej z poniższych funkcji dziedziną i zbiorem wartości jest przedział [0, 1].
Każdy patyk ma długość 1.

ZADANIE 3.b*. Oblicz objętości brył 'pod schodami' dla pozostałych f-schodów.

 

 

ZADANIE 4. Dla których z poniższych funkcji fk, objętość bryły 'pod schodami' jest:

    a)  mniejsza od /2,          b)  równa /2 ?          c)  większa od /2 ?
Uwagi
Dla każdej z poniższych funkcji dziedziną i zbiorem wartości jest przedział [0, 1].
Każdy patyk ma długość 1.

 

 

Dalszy ciąg zadań o szprychach w cylindrze znajdziesz w artykule Szprychy w cylindrze (2)- f-stożki i anty-f-stożki.

 

Powrót na górę strony