Szprychy w cylindrze (3) - f-abażury

Do rysunków 3D użyto apletu www.javaview.de/ Można w nich manipulować myszą.

 

Każda z poniższych powierzchni:
  -  mieści się w cylindrze o promieniu podstawy 1 i o wysokości OO' = 1,
 -  jest zbudowana z patyków-odcinków zaczepionych jednym końcem w okręgu podstawy cylindra,
 -  drugie końce tych patyków zaczepione są w górnej podstawie cylindra.

Patrząc z góry, widzimy, że każda 'szprycha' AO ma w podstawie cylindra odpowiadający jej jeden patyk A'B'.
Przepis na taką powierzchnię jest następujący:

dla zadanej funkcji f (x), określonej na odcinku [0,1],
'szprysze' AO w podstawie, która tworzy z osią OX kąt x ^. 360^o,
odpowiada patyk A'B' leżący w płaszczyźnie AOO', taki że
 A' = A oraz B'  leży w górnej podstawie cylindra w odległości  f (x) od O',
przy czym A'B' przecina OO'  wtedy i tylko wtedy, gdy  f (x) < 0. Gdy f (x) = 1 dla każdego x, to f-abużur jest powierzchnią boczną cylindra.
Gdy f (x) = 0 dla każdego x, to f-abużur jest powierzchnią boczną stożka.
Dla funkcji stałych, dodatnich (różnych od 1), są to powierzchnie boczne stożków ściętych (o wysokości 1).
Ogólnie nazwiemy takie powierzchnie f-abażurami.

Można też myśleć, że powierzchnię f-abażura tworzą przechylone i wydłużone odcinki składające się na powierzchnię boczną cylindra.

 

---

 

Najpierw obejrzymy f-abażury dla najprostszych funkcji (o wartościach nieujemnych), których wykresy są łamanymi. Takie funkcje wygodnie jest opisać, używając pomocniczych funkcji:

h(x)  =  x-[x]     i     g(x)  =  2|h(x)-0,5| .  
Dlaczego dla  f (x)  =  0,5 + 0,25 g(9x)  f-abażur nazywa się 'klasycznym'?

 

 

Dlaczego dla  f (x)  =  0,75 g(x)+ 0,25 g(7x)  f-abażur nazywa się 'kanadyjskim?

Dlaczego dla  f (x)  =  0,75 g(3x)+ 0,25 g(24x)  f-abażur nazywa się 'jesiennym'?

Dlaczego dla  f (x)  =  g(x)  f-abażur nazywa się 'walentynkowym'?

Jak nazwać f-abażury postaci  f (x)  =  g(n ^. x)?

Czym różnią sią f-abażury postaci  f (x) = h(n ^. x)  od f-abażurów postaci  f (x) = g(n ^. x)?

 

---

 

Ciekawsze kształty abażurów dostaniemy dla funkcji f [0,1] [-1, 1], które przyjmują wartości dodatnie i ujemne. Wtedy niektóre otwory f-abażura są 'zacerowane'.
Zobaczmy to na przykładzie funkcji, które są zbudowane z funkcji trygonometrycznych.

 

 

Dla jakich n f-abażury postaci  f (x) = sin(n ^. x)  mają 'zacerowane' wszystkie otwory?

Dla jakich n f-abażury postaci  f (x)  =  sin( n ^. x )  są takie same (przystające), jak
f-abażury postaci  f (x)  =  cos( n ^. x )

Jak nazwać f-abażur dla  f (x)  =  | sin( 2 ^. x ) |?

Czym różnią się f-abażury postaci  f (x)  =  | sin( n ^. x ) | 
od f-abażurów postaci  f (x)  =  sin² ( n ^. x )?

Dla jakich n f-abażury postaci  f (x)  =  0,8 ^. sin( 4 ^. x )  +  0,2 ^. sin( n ^. x )  mają oś symetrii?

 

---

 

Używając pomocniczych funkcji

h (x)  =  2|x - [x] - 0,5|     i     g (x)  =  h (n ^. x) / n . oraz funkcji trygonometrycznych, możemy opisać f-abażury, których otwory mają kształty znane z lekcji geometrii.

 

 

Jaki kształt ma otwór f-abażura dla  f (x) = 1 / ( |sin(x ^. 2)| + |cos(x ^. 2)| )?

Jaki kształt (w zależności od n) ma otwór f-abażura postaci  f (x) = cos(g(0) ^. ) / cos(g(x) ^. ),
gdzie h (x)  =  2|x - [x] - 0,5|     i     g (x)  =  h (n ^. x) / n?

Jaki kształt (w zależności od n) ma otwór f-abażura postaci  f (x) = cos(g(x) ^. ),
gdzie h (x)  =  2|x - [x] - 0,5|     i     g (x)  =  h (n ^. x) / n?

 

---

 

Rozważmy teraz tylko takie funkcje f , które na przedziale [0, 1] przyjmują wartości nieujemne.

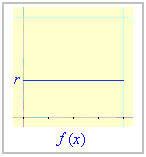Dla funkcji stałej f(x) = r, gdzie 0<r<1, f-abażur jest powierzchnią boczną stożka ściętego, który powstał ze stożka o wysokości H = 1/(1-r). Zrób rysunek i zapisz podobieństwo odpowiednich trójkątów. Zatem objętość bryły pod tym f-abażurem jest równa

/3 ^. 1^{2 .} H   -   /3 ^. r^{2 .} (H-1), co po przekształceniach jest równe ( 1 + r + r² ) / 3. Zauważ, że ostatni wzór jest poprawny również dla r=0, dla r=1, a nawet dla r>1.

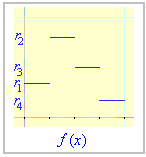Dla funkcji f, która (dla ustalonego n) przyjmuje wartości r_i na przedziałach [i/n, (i+1)/n ), f-abażur jest powierzchnią utorzoną z n powierzchni stożków ściętych. Objętość bryły pod tym f-abażurem jest równa sumie 1/n części objętości stożków ściętych:

1/n ^. (/(1+r₁+r_i²)/3) + 1/n ^. (/3(1+r₂+r₂²)/3) + . . . +          
                                                           + 1/n ^. ((1+r_n+r_n²)/3). Można to zapisać inaczej: ( 1  +  r_i/n  +  r_i²/n ) / 3.

Na podstawie powyższej obserwacji metodami matematyki wyższej nietrudno jest uzasadnić ogólne twierdzenie:

Twierdzenie A
Niech funkcja f przyjmuje na przedziale [0, 1] tylko wartości nieujemne,
niech A oznacza pole pod wykresem tej funkcji na przedziale [0,1]
i niech K oznacza pole pod wykresem funkcji f ² na przedziale [0,1].
Wtedy objętość bryły pod f-abażurem jest równa

( 1 + A + K ) / 3 .

Na tej podstawie można już elementarnie uzasadnić następne twierdzenie:

Twierdzenie B
Niech funkcja g przyjmuje na przedziale [0, 1] tylko wartości nieujemne
i niech n oznacza liczbę naturalną.
Wtedy objętość bryły pod g-abażurem jest równa objętości bryły pod f-abażurem, gdzie

f (x)  =  g ( nx - [nx] ).

Stąd w szczególności:
- równe są objętości brył pod f-abażurami postaci f(x) = 2|nx-[nx] - 1/2|  (obj. = 11/18),
- równe są objętości brył pod f-abażurami postaci f(x) = sin(2nx)/2 + 1/2  (obj. = 5/8),
- równe są objętości brył pod f-abażurami postaci f(x) = | sin(nx) |  (obj. = /2 + 2/3).

 

---

---

 

Jeśli zainteresował Cię ten temat, przeczytaj koniecznie jego ciąg dalszy w artykule Szprychy w cylindrze (4) - f-ślimaki.