|
Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą. |
Sześcian wygląda jednakowo z każdej strony: z obu profili, z tyłu i 'en face', a także od góry i z dołu. To lepiej niż posąg mitycznego Światowida, który miał zaledwie cztery jednakowe twarze patrzące w różne strony świata. Są też inne bryły o sześciu jednakowych obliczach. Nazwiemy je światowidami super 3D. Obejrzyj przykłady.
(Czwarta z poniższych brył jest przybliżeniem kostki Mengera, a na jej ścianach widać przybliżenia dywanu Sierpińskiego.)
Zapraszamy do zabawy w projektowanie własnych światowidów super 3D.
Na siatce n×n wyklikaj swój projekt P, t.j. widok z profilu (a jednocześnie 'en face' i z góry) projektowanej bryły. Automat z sześcianu n×n×n
Jak mówił Michał Anioł: 'Rzeźbi Natura, ja usuwam tylko to, co zbędne'.
Uwaga 1
Nie każdy projekt P można zrealizować. Co to znaczy i kiedy tak jest, omówimy nieco później.
Pracownia projektowa światowidów super 3D
Projekt P (klikaj)
siatka n×n, n= <13
UWAGA 2
Sprecyzujmy jak działa nasz automat.
Przyjmijmy oznaczenia dla projektu P na siatce n×n:
- kratkę z P oznaczamy współrzędnymi jej prawego górnego wierzchołka, czyli lewą dolną kratkę oznaczamy (1,1), a lewą górną (1,n),
- blok w sześcianie n×n×n oznaczamy podobnie, tzn. (1,1,1) oznacza blok o wierzchołku (1,1,1) i przekątnej (0,0,0)-(1,1,1), a (2,3,5) oznacza blok o wierzchołku (2,3,5) i przekątnej (1,2,4)-(2,3,5).
Gdy w projekcie P nie ma kratki (2,4), to usuwamy
z sześcianu n×n×n
wszystkie bloki, które:
- mają współrzędne postaci (2,y,4); dzięki temu, gdy patrzymy z przodu, wzdłuż osi OY, widzimy puste okienko w kratce (2,4),
- mają współrzędne postaci (x,2,4); dzięki temu, gdy patrzymy z boku, wzdłuż osi OX (przeciwnie do jej zwrotu), widzimy puste okienko w kratce (2,4),
- mają współrzędne postaci (2,4,z); dzięki temu, gdy patrzymy z góry, wzdłuż osi OZ (przeciwnie do jej zwrotu), widzimy puste okienko w kratce (2,4).
Powtarzamy to dla wszystkich nie zaznaczonych kratek projektu P.
Efekt działania nieco innego algorytmu zobaczysz na prawym rysunku, zaznaczając opcję [inna wersja]. Otrzymujemy wtedy symetryczne odbicie poprzedniej bryły. Względem jakiej płaszczyzny jest ono odbite?
Dalej będziemy zajmować się tylko tymi bryłami, które powstały według opisanego wyżej algorytmu (odhacz opcję [inna wersja]).
Zadanie 1.
Dla podanego projektu wyobraź sobie całego światowida super 3D i oblicz:
- pole p projektu (jednostką jest kratka),
- liczbę b bloków, z których składa się cała rzeźba,
- pole ś całej rzeźby (jednostką jest kratka).
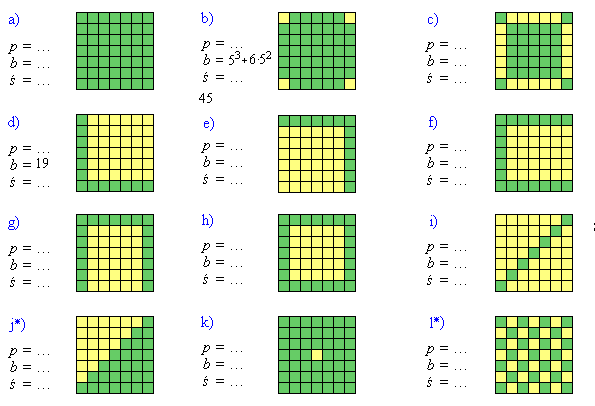
Zadanie 2. W Zadaniu 1. w niektórych przykładach mamy:
Nie dla każdego projektu P istnieje światowid super 3D.
Te projekty P, dla których istnieje bryła, która z każdej strony wygląda jak P, nazwiemy projektami realizowalnymi.
Zadanie 3.
Ile jest realizowalnych jednokratkowych (p=1) projektów na siatce 5×5?
Zadanie 4.
Czy jeśli projekt jest symetryczny względem przekątnej (0,0)-(n×n), to jest realizowalny?
Zadanie 5.
Niech dwa projekty P1 i P2 nie mają wspólnych kratek i w sumie pokrywają całą siatkę 5×5.
Czy wtedy:
a) oba są realizowalne?
b) co najmniej jeden z nich jest realizowalny?
Zadanie 6*.
Ile jest realizowalnych dwukratkowych (p=2) projektów na siatce 9×9 ?
PROBLEM *. Znajdź warunki konieczne i wystarczające do tego, by projekt był realizowalny.
Nim podamy rozwiązanie tego problemu, warto znaleźć częściowe odpowiedzi. Podamy kilka obserwacji.
Obserwacja 1
Jeśli projekt zawiera kratki z lewej i prawej kolumny oraz nie zawiera żadnej kratki z górnego wiersza siatki, to jest nierealizowalny.
Oczywiście zachodzi również
Obserwacja 1'
Jeśli projekt zawiera kratki z lewej i prawej kolumny oraz nie zawiera żadnej kratki z dolnego wiersza siatki, to jest nierealizowalny.
Jeśli projekt zawiera kratki z dolnego i górnego wiersza oraz nie zawiera żadnej kratki z lewej lub prawej kolumny siatki, to jest nierealizowalny.
Można znaleźć też warunki wystarczające.
Obserwacja 2
Jeśli projekt zawiera cały dolny wiersz i całą lewą kolumnę siatki, to jest realizowalny.
Można tę obserwację uogólnić.
Można zobaczyć, że zachodzi:
Zadanie 7. Znajdź przykład takiego realizowalnego projektu, który nie spełnia żadnego z warunków podanych w obserwacjach: 2, 2', 3.
(tylko dla dorosłych, tzn. znających pojęcia relacji i złożenia relacji)




