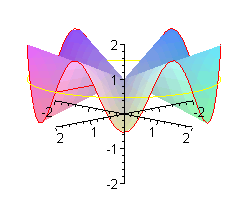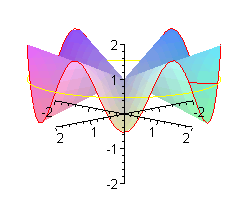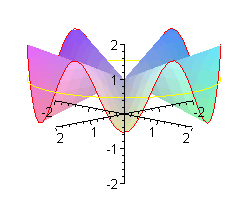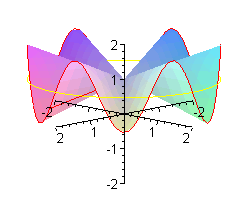
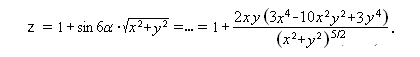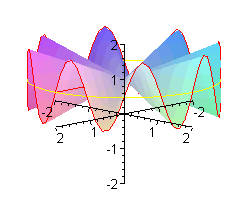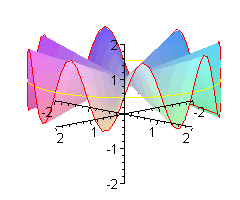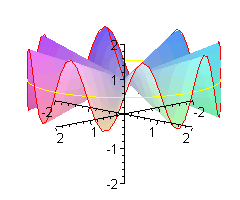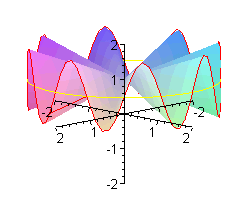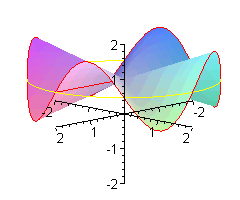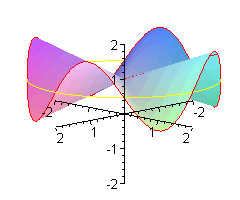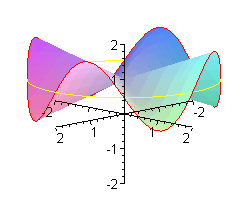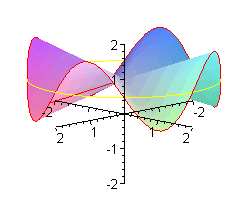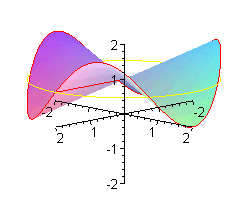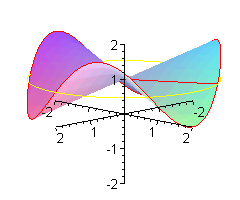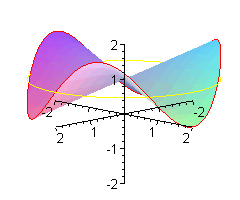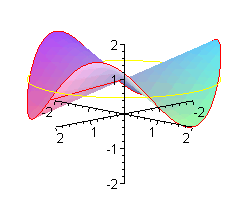 Co to jest 'małpie siodło'? Oprócz wzoru z = x ( x 2 - 3y 2 )
znalazłem kiedyś w Internecie takie oto wyjaśnienie:
Co to jest 'małpie siodło'? Oprócz wzoru z = x ( x 2 - 3y 2 )
znalazłem kiedyś w Internecie takie oto wyjaśnienie:
Małpa to nie człowiek
i swój... ogon ma,
nie wystarczą jej do jazdy w siodle,
tylko strzemiona dwa.
Potrzebuje jeszcze trzecie,
na ogon, wszak go ma.
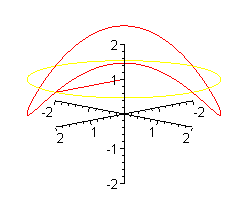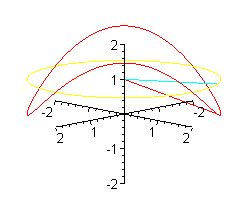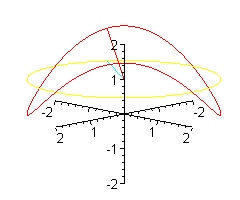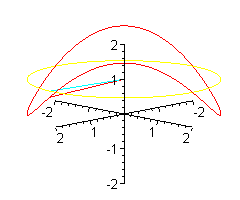
Poniżej pokazujemy, jak wymyśla się takie wzory, i dla małpy, i dla biedronki.
Jak wiadomo biedronka ma n = 6 nóg. W zwykłym siodle jest jej bardzo niewygodnie - musi trzymać po trzy nóżki razem. Wymodelujemy jej takie siodło, że każdą nóżkę będzie trzymała oddzielnie.
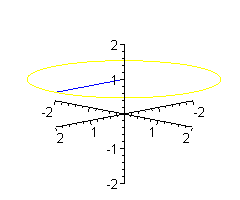
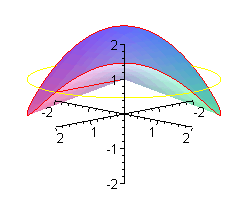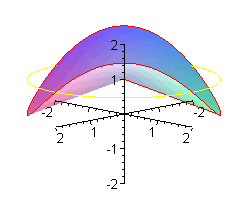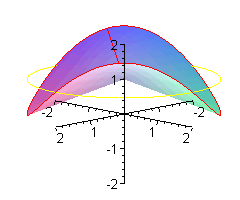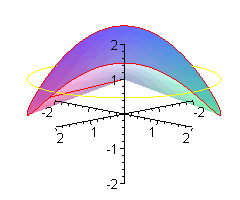
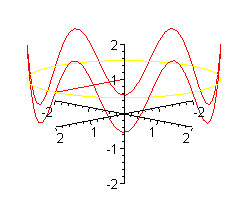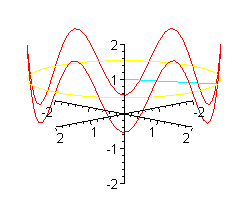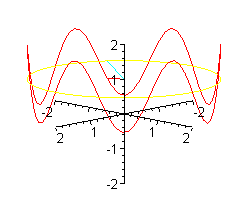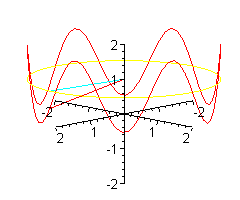
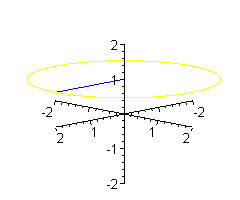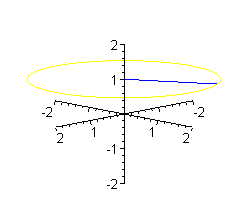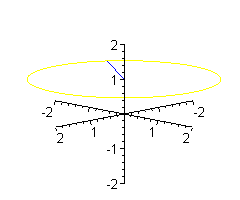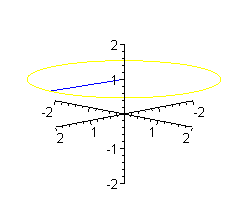
Można sobie wyobrażać, że koło o środku w punkcie (0,0,1), prostopadłe do osi OZ jest 'wymiatane' obracającym się promieniem.
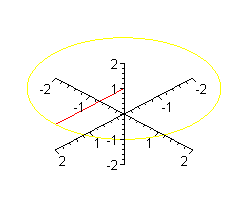
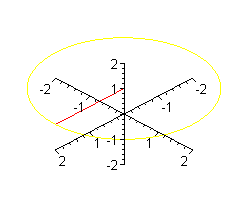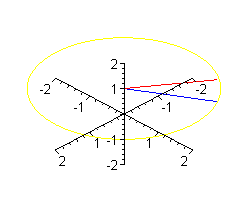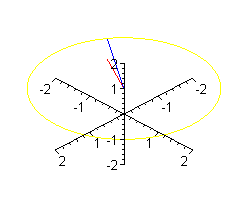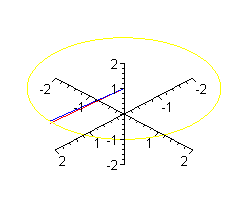
Można sobie wyobrazić patyk, obracający się podobnie jak promień
wokół osi OZ, przy czym w trakcie obrotu
patyk zmienia nachylenie - na przemian unosi się i opada (przy czym jeden koniec tkwi stale w punkcie (0,0,1)).
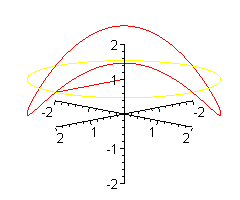
Patyk może unosić się i opadać szybciej.
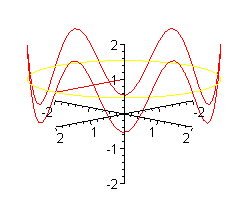
Patyk może unosić się i opadać jeszcze szybciej.

Jeszcze nie widzisz?
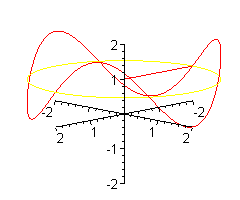
Dla małpy powinien wznosić się i opadać trochę wolniej.
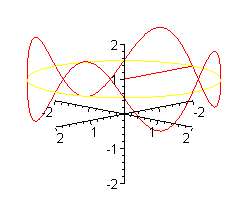
Dla czworonogów też znajdzie się sposób.

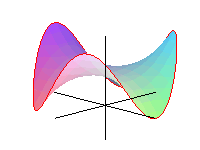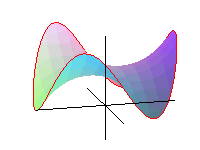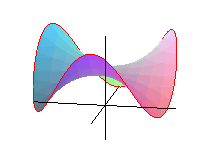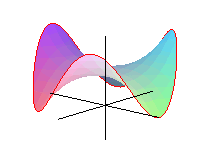
Siodło classic.
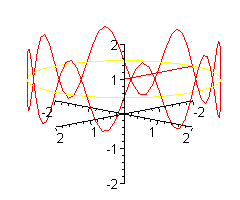
Siodło dla pająka.
Jak opisać wzorem takie siodła?
Jakie równanie spełniają współrzędne punktu (x,y,z), leżącego na siodle?
Dla ustalenia uwagi myślmy o siodle dla małpy, n = 3.
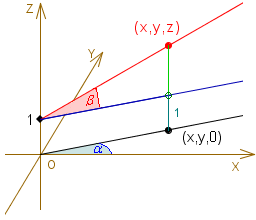 Kluczowa sprawa
Kluczowa sprawa
Zatem i nachylenie, i tg
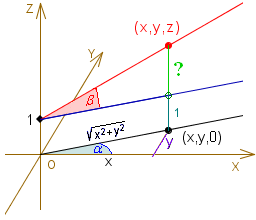 By wyznaczyć z, wystarczy znaleźć długość
zielonego pionowego odcinka.
By wyznaczyć z, wystarczy znaleźć długość
zielonego pionowego odcinka.
Nie jest to jeszcze ostateczny wzór, bowiem oprócz współrzędnych x,y,z występuje w nim kąt
![]() .
Nie widać też takiej prostoty jak we wzorze z = x ( x 2 - 3y 2 ) .
.
Nie widać też takiej prostoty jak we wzorze z = x ( x 2 - 3y 2 ) .
Uwaga (tylko dla dorosłych)
Można 'pozbyć' się kąta
![]() ,
korzystając z zależności
tg
,
korzystając z zależności
tg![]() = y/x.
Otrzymujemy wtedy
= y/x.
Otrzymujemy wtedy
![]()
Jednak trudno taki wzór uznać za elegancki.
Innym sposobem jest skorzystanie ze wzorów trygonometrycznych.
Z tablic matematycznych odczytujemy:
sin 3![]() =
3 sin
=
3 sin![]() cos2
cos2![]() -
sin3
-
sin3![]() =
sin
=
sin![]() (3 cos2
(3 cos2![]() - sin2
- sin2![]() )
,
)
,
a z rysunku
![]()
Wstawiając te zależności (i wykonując przekształcenia), otrzymujemy wzór
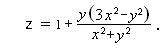
Uwaga (tylko dla dorosłych)
Uzyskane siodła są trochę niewygodne.
Wygodniejsze można zrobić, wyginając patyki w parabole, lub jeszcze bardziej.
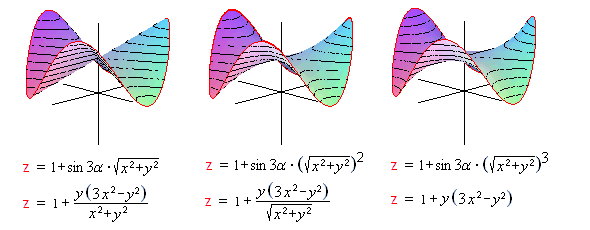 O! Ostatni wzór małpiego siodła jest prawie taki, jak te w Internecie.
O! Ostatni wzór małpiego siodła jest prawie taki, jak te w Internecie.
Biedronkom też można zrobić wygodniej, to znaczy bardziej wygładzić centralny punkt siodła.
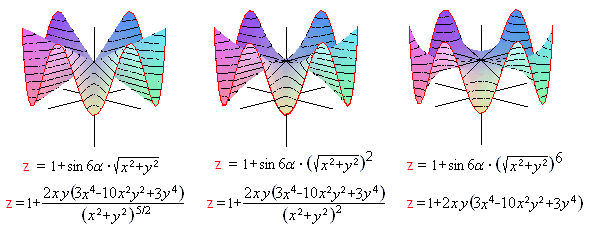
Pytania kontrolne
- Jaki jest 'elegancki' wzór siodła modelu 'classic'?
- Jakie siodło dostaniemy, wstawiając do wzoru n = 1 ?
Uwaga. Uzyskane wzory są tylko jednym z możliwych sposobów opisu takich kształtów.
Powyżej pokazaliśmy, jak szukać w miarę prostego i eleganckiego opisu figur (powierzchni) o ciekawych kształtach.
Powyższe rozważania nie wyjaśniły natomiast dlaczego matematycy zajmują się siodłami, w dodatku dla całego ogrodu zoologicznego. Czyżby nie mieli nic lepszego do roboty?
Ogólnikowa odpowiedź może być następująca:
Siodła są ciekawe, bo są najprostszymi modelami 'dziwnych' zachowań powierzchni. Przyroda daje o wiele bardziej skomplikowane przykłady (wystarczy popatrzeć na pofałdowane góry lub na falujące morze). By móc je opisać, trzeba zrozumieć najpierw najprostsze sytuacje - na przykład takie, jak powyższe siodła.