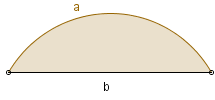
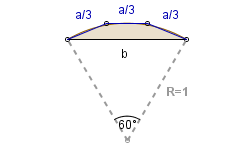
 Na rysunku widać odcinek koła, to znaczy jeden z dwóch obszarów ograniczonych okręgiem i cięciwą tego okręgu. Będziemy rozważać tylko mniejszy z tych dwóch obszarów, czyli taki, że środek koła nie leży w jego wnętrzu. Ponadto zakładamy, że znane są długości: a - łuku i b - cięciwy.
Na rysunku widać odcinek koła, to znaczy jeden z dwóch obszarów ograniczonych okręgiem i cięciwą tego okręgu. Będziemy rozważać tylko mniejszy z tych dwóch obszarów, czyli taki, że środek koła nie leży w jego wnętrzu. Ponadto zakładamy, że znane są długości: a - łuku i b - cięciwy.
gdy dane są wielkości a i b ?
 Pomysł 1
Pomysł 1
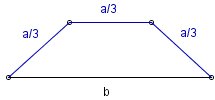
Znajdziemy wzór na pole P1 trapezu równoramiennego o dłuższej podstawie b i pozostałych bokach długości a/3. Taki trapez nieźle przybliża odcinek koła, zatem P1 będzie PRZYBLIŻONYM wzorem na pole odcinka koła.
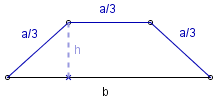 Z tw. Pitagorasa wyznaczamy wysokość takiego trapezu:
Z tw. Pitagorasa wyznaczamy wysokość takiego trapezu:
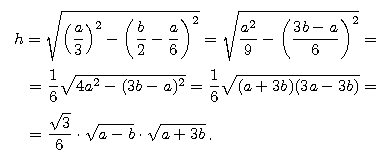 Stąd pole jest równe
Stąd pole jest równe
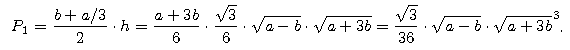
Mamy zatem PRZYBLIŻONY wzór na pole odcinka koła:
![]()
Jak dobre jest to przybliżenie? Sprawdźmy.
Zadanie 1. Wypełnij opis poniższych odcinków kół (P1 oznacza przybliżone pole, a P - dokładne).
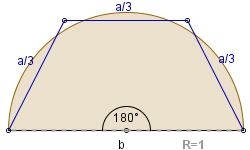 |
a = . . . . . b = . . . . . P = P1 |
błąd względny (w %):
(P1 - P) / P |
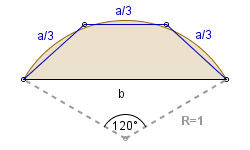 |
a = . . . . . b = . . . . . P = . . . . . P1 |
błąd względny (w %):
(P1 - P) / P |
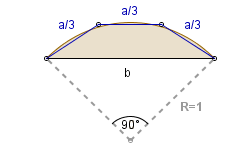 |
a = . . . . . b = . . . . . P = . . . . . P1 |
błąd względny (w %):
(P1 - P) / P |
 |
a = . . . . . b = . . . . . P = . . . . . P1 |
błąd względny (w %):
(P1 - P) / P |
Uwaga 1. Można uzasadnić, że 0,9 . P < P1 < P, czyli że obliczając pole ze wzoru P1, uzyskamy błąd względny mniejszy niż 10-procentowy.
Zadanie 2*. Uzasadnij, że wśród trapezów równoramiennych o obwodzie a+b i jednej podstawie długości b (b < a), największe pole ma trapez o ramionach długości a/3.
Zadanie 3*. Uzasadnij, że wśród czworokątów o obwodzie a+b i jednym boku długości b (b < a), największe pole ma trapez o podstawach długości b i a/3 oraz ramionach długości a/3.
Pomysł 2
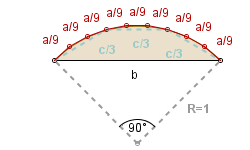
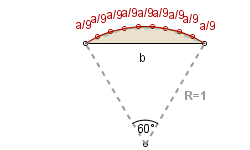
Niech c będzie liczbą mniejszą od a o (a-b)/9,czyli niech c = 8/9 . a + 1/9 . b.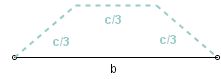 Odcinek koła przybliżymy dziesięciokątem zbudowanym w opisany niżej sposób.
Odcinek koła przybliżymy dziesięciokątem zbudowanym w opisany niżej sposób.
Najpierw budujemy trapez równoramienny o podstawie długości b
i pozostałych bokach długości c/3.
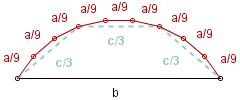 Na tych trzech bokach budujemy trapezy równoramienne o podstawach długości c/3 i pozostałych bokach długości a/9.
Na tych trzech bokach budujemy trapezy równoramienne o podstawach długości c/3 i pozostałych bokach długości a/9.
Pole P2 tak zbudowanego dziesięciokąta łatwo obliczymy, stosując dwa razy poprzedni wzór:
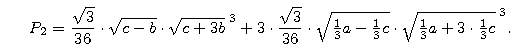
Dalej już tylko wstawiamy wartość c i nieco mozolnie przekształcamy.
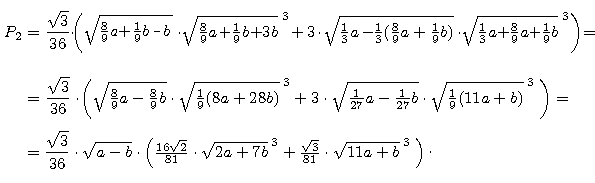
Mamy zatem drugi PRZYBLIŻONY wzór na pole odcinka koła:
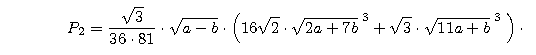
Jak dobre jest to przybliżenie? Sprawdźmy.
Zadanie 4. Wypełnij opis poniższych odcinków kół (P2 oznacza przybliżone pole, a P - dokładne).
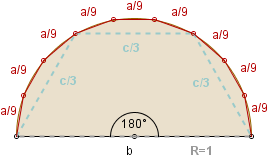 |
a = . . . . . b = . . . . . P = P2 |
błąd względny (w %):
(P2 - P) / P |
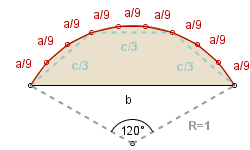 |
a = . . . . . b = . . . . . P = . . . . . P2 |
błąd względny (w %):
(P2 - P) / P |
 |
a = . . . . . b = . . . . . P = . . . . . P2 |
błąd względny (w %):
(P2 - P) / P |
 |
a = . . . . . b = . . . . . P = . . . . . P2 |
błąd względny (w %):
(P2 - P) / P |
Uwaga 2. Można uzasadnić, że 0,98979 . P < P2 < P, czyli że obliczając pole ze wzoru P2,uzyskamy błąd względny mniejszy niż 1.1-procentowy.
Uwaga 3. Powyższe rysunki sugerują, że rozważane dziesięciokąty są wpisane w odcinki kół, że ich wierzchołki leżą na łukach tych odcinków. Nie jest to prawda. To tylko efekt dobrego przybliżenia i niedokładności rysunków. Można uzasadnić, że niektóre z wierzchołków muszą leżeć poza odcinkami kół (w przeciwnym wypadku obwody dziesięciokątów byłyby mniejsze od obwodów odcinków kół).
Pomysł 3
Można uzasadnić, że 0,98979 . P < P2 < 0,99365 . P .
Zauważmy, że 1,0083 . 0,98979 = 0,998005257 , 1,0083 . 0,99365 = 1.001897295.
Niech 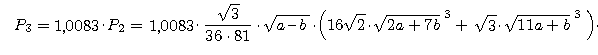 Jest to trzeci PRZYBLIŻONY wzór na pole odcinka koła.
Jest to trzeci PRZYBLIŻONY wzór na pole odcinka koła.
Mamy: 0,998 . P < P3 <1,002 . P,
czyli że obliczając pole ze wzoru P3, uzyskamy błąd względny mniejszy niż 2 promile.
Powyższe rozważania mogą nasuwać następne pytania:
- Czy można uzyskać jeszcze lepsze przybliżenia?
- Jak badać błędy względne (nie tylko dla niektórych odcinków kół)?
- Dlaczego jest tu mowa o przybliżeniach, czy nie prościej podać DOKŁADNY wzór?
Odpowiedzi wymagają znajomości trygonometrii. Warto przeczytać tekst Odcinek koła (2).
Powyższy tekst powstał po przeczytaniu artykułu Marka Kordosa 'Rozprawka o metodzie', Delta 7 (2015). Gorąco polecamy jego lekturę.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


