|
Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą. |
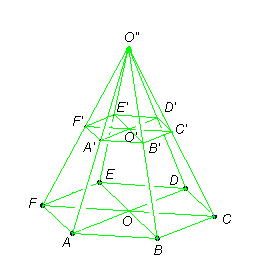
Rzecz będzie się działa w ostrosłupie prawidłowym o wysokości OO'' = 2 i podstawie ABCDEF, której bok ma długość 1. Przez O', A', B', C',... oznaczmy punkty będące środkami odcinków: OO'', AO'', BO'', CO'',....
Dla pewnej kolekcji K wyróżnionych punktów ostrosłupa, niech W = W(K) oznacza najmniejszy wypukły wielościan zawierający punkty z K. Wypukły oznacza: bez dziur i wklęsłości.
Na przykład dla
Ma on:
w = 7 wierzchołków,
k = 12 krawędzi,
s = 7 ścian.
Uwaga: nie wszystkie punkty z K są wierzchołkami (w tym przykładzie nie jest nim O).
Bryła W ma objętość V = 7 ![]() / 12.
Można to obliczyć kilkoma sposobami.
Na przykład tak:
płaszczyzna ADD'A' odcina z W ostrosłup o wierzchołku E, resztę można podzielić płaszczyzną ABD' na dwa ostrosłupy o wierzchołkach B i D'.
/ 12.
Można to obliczyć kilkoma sposobami.
Na przykład tak:
płaszczyzna ADD'A' odcina z W ostrosłup o wierzchołku E, resztę można podzielić płaszczyzną ABD' na dwa ostrosłupy o wierzchołkach B i D'.
W innych przykładach łatwiej może być obliczać objętości części ostrosłupa usuwanych przy 'rzeźbieniu' W.
Na poniższym rysunku możesz przetestować swoją wyobraźnię przestrzenną.















Proponujemy teraz kilka zadań. Uwaga, obliczanie objętości może być w niektórych wypadkach żmudne.
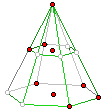 Zadanie 1.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
Zadanie 1.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
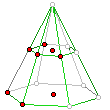 Zadanie 2.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
Zadanie 2.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
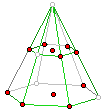 Zadanie 3.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
Zadanie 3.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym zaznaczone punkty.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 4. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 4'. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 4''. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 5. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 5'. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 5''. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 6. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 6'. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 7. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 7'. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 7''. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 8. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 8'. Niech W będzie najmniejszym wypukłym wielościanem zawierającym punkty:
Zadanie 9.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym środki wszystkich krawędzi ostrosłupa.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 9'.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym środki wszystkich krawędzi i wierzchołek ostrosłupa.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 10*.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym środki wszystkich ścian ostrosłupa.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 10'*.
Niech W będzie najmniejszym wypukłym wielościanem zawierającym środki wszystkich ścian i wierzchołek ostrosłupa.
Dla W mamy:
w = . . . . . .
k = . . . . . .
s = . . . . . .
V = . . . . . .
Zadanie 11**. Niech W będzie najmniejszym wypukłym wielościanem zawierającym pewne spośród punktów A, B, C, D, E, F, A', B', C', D', E', F', O, O', O'' ostrosłupa.
a) Jaka może być liczba w jego wierzchołków?
b) Jaka może być liczba k jego krawędzi?
c) Jaka może być liczba s jego ścian?
d) Jaka jest najmniejsza (niezerowa) objętość V?



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


