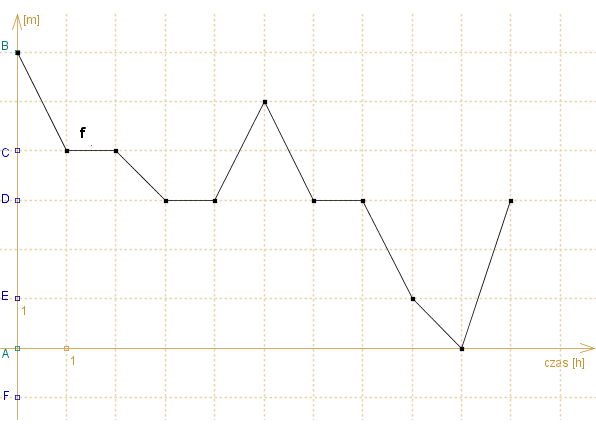
Ślimak Filip w czasie 10-godzinnej wycieczki spacerował wzdłuż prostej AB. Jego wędrówkę przedstawia poniższy wykres funkcji f, ukazujący pozycję Filipa w zależności od czasu. (Pozycja jest określana jako odległość od punktu A.)
ZADANIE 1.
a)
Podaj f (1), f (1,5), f (3,5),
czyli podaj pozycję Filipa po: godzinie, półtorej godziny, trzech i pół godzinach od startu.
b)
W jakiej odległości od startu Filip zakończył wędrówkę?
c) Ile czasu zajęły mu odpoczynki na trasie?
d)
Ile razy Filip przechodził przez środek odcinka AB? W której godzinie wycieczki?
e)
W której godzinie przebył największy dystans?
f)
Ile metrów przebył w czasie całej wycieczki?
g)
Po jakim czasie osiągnął półmetek (tzn. po jakim czasie przebył połowę całego dystansu wędrówki)?
h)
Jak długo był w odległości nie większej niż jeden metr od punktu B?
i)
Jak długo był w odległości większej niż jeden metr od punktu startu?
Na poniższym rysunku przedstawiono wykres funkcji f - wędrówki ślimaka Filipa oraz wykres funkcji gP opisującej odległość Filipa od punktu P prostej AB, w czasie 10-godzinnej wycieczki. Przesuwając P, zobaczysz inne takie funkcje.
ZADANIE 2.
a) Naszkicuj wykresy funkcji:
gC ,
gD ,
gE ,
gF , dla podanej na wykresie funkcji f .
b) Naszkicuj wykresy funkcji:
gC ,
gD ,
gE ,
gF , dla podanej na wykresie funkcji f .
ZADANIE 3.
a)
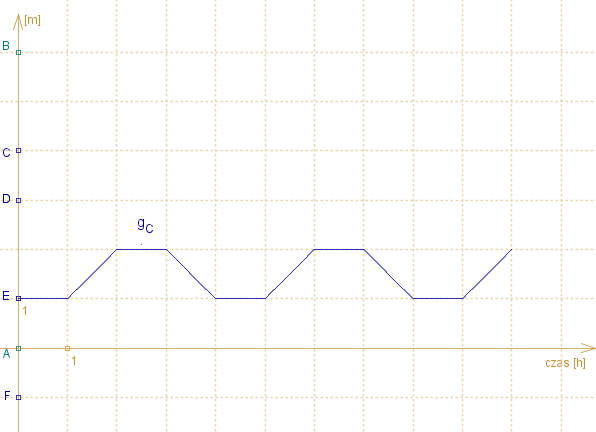
Na rysunku pokazano wykres funkcji gC powstały dla pewnej funkcji f.
Naszkicuj wykres funkcji f (uwaga: jest wiele możliwości).
b)
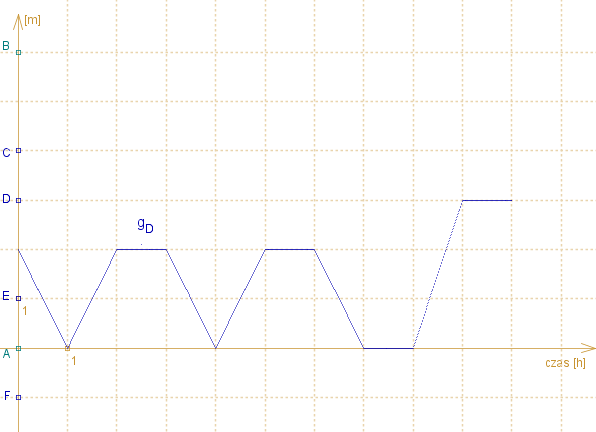
Na rysunku pokazano wykres funkcji gD powstały dla pewnej funkcji f.
Naszkicuj wykres funkcji f (uwaga: jest wiele możliwości).
c)
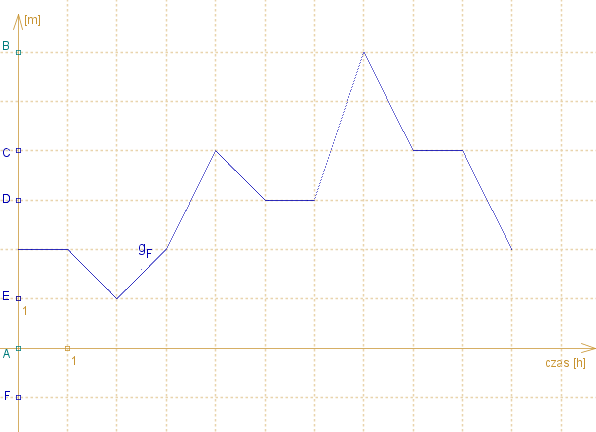
Na rysunku pokazano wykres funkcji gF powstały dla pewnej funkcji f.
Naszkicuj wykres funkcji f .
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
