Każdy wie, że różnica to wynik odejmowania liczb. Jest to również wynik odejmowania zbiorów. W artykule mowa będzie jednak o zupełnie innej różnicy, i o tym, do czego można ją wykorzystać. Ten sam temat można 'przerobić' w zadaniach zebranych w artykule Różnica symetryczna (w zadaniach).
W wypowiedziach:
'Te dwie kolekcje (monet) różnią się bardzo...',
'Te dwa zestawy (zadań) można uznać za takie same, różnica jest nieistotna...
'Te dwa zbiory (znaczków) są zbliżone, nie bardzo się różnią...',
mowa jest o 'różnicach' zbiorów lub kolekcji. W każdym zdaniu sens tego słowa jest trochę inny.
W matematyce też jest wiele 'różnic', tzn. jest wiele pojęć oddających sens tego słowa.
Chyba najprostszym z nich jest pojęcie różnicy symetrycznej zbiorów.
Różnica symetryczna zbiorów A i B jest zbiorem tych elementów tych zbiorów, które należą do dokładnie jednego z nich.
Symbol 
oznacza
różnicę symetryczną, piszemy:
B .
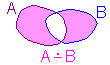Na lewym diagramie zaznaczono zbiory A i B,a na prawym - ich różnicę symetryczną.
Przykłady
{1, 3, 4, 6, 7, 9}
{3, 5, 6, 7, 8, 9} = {1, 4, 5, 8} ,
{1, 2, 3, 4, 5, 6}
{4, 5, 6, 7, 8, 9} = {1, 2, 3, 7, 8, 9} ,
{3, 1, 4, 2, 5, 9}
{1, 2, 9, 8, 5, 6} = {3, 4, 6, 8} ,
gdy A = zbiór liczb < 32 podzielnych przez 6 i
B = zbiór liczb < 32 podzielnych przez 10,
to
A B
= { 6, 10, 12 , 18, 20, 24 } ,
gdy A = koło, B = wnętrze koła A, to A
B = okrąg koła A .
Odległość zbiorów
Można mierzyć odległość punktów płaszczyzny lub odległość liczb na osi.
A jak zmierzyć odległość zbiorów?
Policzenie liczby elementów różnicy symetrycznej zbiorów A i B jest sposobem na zmierzenie odległości tych zbiorów (pod warunkiem, że A i B są skończone).
Na przykład:
zbiory {1, 2, 3, 4, 5, 6}, {4, 5, 6, 7, 8} są odległe o 5, bo różnią się pięcioma elementami,
a zbiory {1, 3, 4, 5, 6}, {1, 3, 5, 6, 8} są odległe o 2, bo różnią się 2 dwoma elementami.
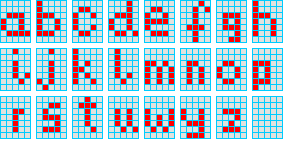Obok przedstawiono pewien sposób reprezentacji liter alfabetu łacińskiego. Można myśleć, że litery są zbiorami kwadratów (poszczególne kwadraty można opisać tak, jak w grze w okręty).
Wtedy 'a' i 'b' są odległe o 7, bo różnica symetryczna tych zbiorów ma 7 kwadratów.
Litery 'u' i 'w' są odległe o 18, a
odległość 'a' i 'w' jest równa 13.
Można sprawdzić, że odległości liter w tym zestawie są co najmniej równe 3. Nie ma w nim bliższych liter. To może mieć znaczenie praktyczne.
Gdy na łączach nastąpi błąd i w kodzie przekazywanej litery jeden z kwadratów 'zgaśnie', albo jeden się dodatkowo się 'zapali' (jak w żarówkach LED), otrzymamy znak, np. taki jak na rysunku obok, nie będący żadną literą zestawu. Jednak łatwo rozpoznać, że ten znak jest zniekształconym 'a'. Od 'a' różni się o 1, natomiast od 'd' różni się o 2. Od innych liter ten znak jest jeszcze bardziej odległy. Widzi to łatwo każdy z nas, ale może też to "zauważyć" automat, który nie 'widzi'. Algorytm poprawiania zniekształconych znaków polega zatem na znajdowaniu litery z zestawu, która jest w najmniejszej odległości od danego znaku.
Ilustruje to (ważne w informatyce) pojęcie kodów samokorygujących. Oczywiście nie dotyczy ono kodów pokazanego zestawu liter, lecz informacji zapisanych za pomocą bitów. Jednak zasada działania tych kodów jest mniej więcej ta sama.
Dla figur na płaszczyźnie powyższy sposób mierzenia odległości nie jest przydatny, bo zazwyczaj rozważamy figury będące zbiorami nieskończonymi punktów. Dla pewnych figur odległość można określić następująco:
Przez odległość figur A i B będziemy rozumieć pole ich różnicy symetrycznej, czyli
B ) .
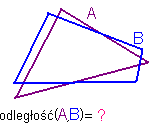
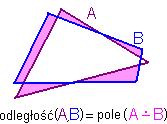
Na rysunkach zaznaczono:
trójkąt A, czworobok B
i ich odległość.
Ćwiczenie 1. Znajdź największą odległość dwóch trójkątów równobocznych wpisanych w dane koło o promieniu 1.
Ćwiczenie 2. Znajdź największą odległość dwóch sześciokątów foremnych wpisanych w dane koło o promieniu 1.
Za pomocą tego pojęcia zdanie:
,
to odległość(Wn, K) 0 .'
Do czego to podobne?
|
dla liczb całkowitych mamy:
a + b = b + a (a + b) + c = a + ( b + c ) a + 0 = a a + (-a) = 0 |
Różnica symetryczna ma podobne własności jak zwykłe dodawanie:
- przemienność (oczywista)
A B =
B A ,
- łączność (można żmudnie sprawdzić na diagramach)
( A B )
C =
A ( B
C ) ,
- odpowiednikiem 0 jest zbiór pusty:
A
= A ,
- oraz (co jest nieco zaskakujące)
A A =
,
czyli można powiedzieć: A jest przeciwne do A .
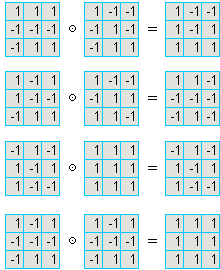Rozważmy wszystkie szachownice o dziewięciu polach wypełnione
liczbami 1 lub -1. Mnożąc liczby z odpowiadających pól dwóch szachownic, tworzymy nową szachownicę, jest to wynik działania 
na tych szachownicach.
Własności są podobne jak własności dodawania liczb,
np. odpowiednikiem 0 jest szachownica złożona z samych 1.
Gdy pola z -1 zaznaczymy kolorem i pomyślimy, że szachownice są zbiorami kolorowych kwadratów, to zobaczymy, że teraz
jest dokładnie tym samym co .
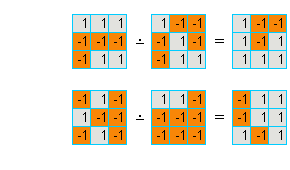
Zatem wszystkie podzbiory zbioru {1, 2, 3,... , 9}
z działaniem
tworzą taką samą strukturę jak wszystkie 3×3 szachownice, wypełnione 1 i -1, z działaniem .
Uwaga (tylko dla dorosłych). Na studiach matematycznych mówi się, że te struktury są izomorficzne z grupę abelową Z29.
Związki z innymi działaniami na zbiorach
Na poniższych diagramach zilustrowane są inne operacje na zbiorach:
B
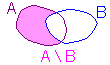
można zapisać na kilka sposobów:
A B =
(A \ B ) 
(B \ A ) ,
A
B =
(A B) \
(A 
B) ,
A
B =
(A \ (A B) )
(B \ (A B) ) .
Ćwiczenie 3.
W poniższych przykładach zaznacz na diagramach opisane zbiory.
W których miejscach znak zapytania '?' można zastąpić znakiem równości '=' ?
 |
( A B )
C
| ? | ( A C )
( B C )
| |
|
( A B )
C
| ? | ( A C )
( B C )
| |
|
( A B )
C
| ? | ( A C )
( B C )
| |
|
( A B )
C
| ? | ( A C )
( B C )
| |
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
