Trzydziestościan rombowy wielki

W rozdziale poświęconym wielościanom Catalana opisany został m.in. wielościan dualny do dwudziesto-dwunastościanu, czyli trzydziestościan rombowy. Poniżej prezentujemy jedno z wielu stożkowań (ang. stellation) tego wielościanu, czyli trzydziestościan rombowy wielki.

Zacznijmy jednak od spojrzenia na kompozycję 5 sześcianów (rys. 1).

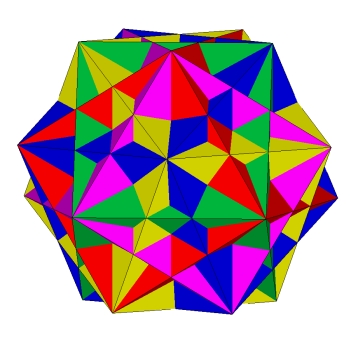
rys. 1

Jest to jedna z pięciu istniejących foremnych kompozycji wielościanów. Łatwo zauważyć, że wierzchołki tej kompozycji pokrywają się z wierzchołkami dwunastościanu foremnego, a krawędzie sześcianów są przekątnymi ścian tego dwunastościanu. To spostrzeżenie pozwala narysować linie, wzdłuż których daną ścianę kompozycji przecinają inne jej części. Wystarczy podzielić każdą krawędź w taki sposób, w jaki dzielą się przekątne pięciokąta foremnego (czyli w stosunku złotym) i, patrząc na rysunek 1, prowadzić odpowiednie odcinki (rys. 2).

rys. 2

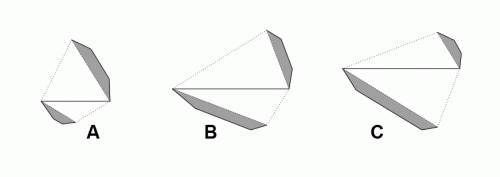
Zacieniowane fragmenty ściany to widoczne na zewnątrz części kompozycji. Stąd już prosta droga do przygotowania elementów siatki kompozycji pięciu sześcianów. Przedstawione są one na rysunku 3. Część C jest lustrzanym odbiciem części B. Kliknięcie w rysunek otwiera w nowym oknie zestaw elementów potrzebnych na jeden sześcian.

rys. 3

Do wykonania całości potrzeba 5 kopii tego zestawu (po jednej w każdym z 5 kolorów). Linie przerywane oznaczają krawędzie wklęsłe. Trzeba jednak zwrócić uwagę na fakt, że wykonanie modelu 5 sześcianów wymaga nie tylko dużej staranności, ale niezbędny jest też pewien wewnętrzny stelaż. W przeciwnym razie model będzie bardzo podatny na odkształcenia. Przykładowy sposób rozwiązania tych trudności został przedstawiony w książce W krainie wielościanów. Zrób sobie bryłkę.

Powróćmy jednak go głównego tematu artykułu, czyli konstrukcji pewnego stożkowania trzydziestościanu rombowego. Spójrzmy na rysunek 4 (będacy kopią poprzedniego rysunku tylko inaczej pocieniowaną).

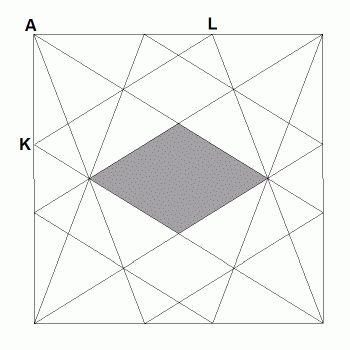
rys. 4

Na kwadratowej ścianie wycięty został romb, którego stosunek przekątnych jest równy AL/AK, czyli złotej liczbie (to jest około 1,618). Ponieważ kompozycja 5 szescianów ma 30 ścian kwadratowych, prowadzi to do bryły ograniczonej 30 rombami o stosunku przekątnych będącym złotą liczbą. To jest właśnie trzydziestościan rombowy. Zatem kompozycję pięciu sześcianów możemy zinterpretować jako jedno ze stożkowań tego trzydziestościanu, a rysunek 4 przedstawia fragment diagramu stellacyjnego. Przedłużmy linie z rysunku 4, otrzymując rysunek 5.

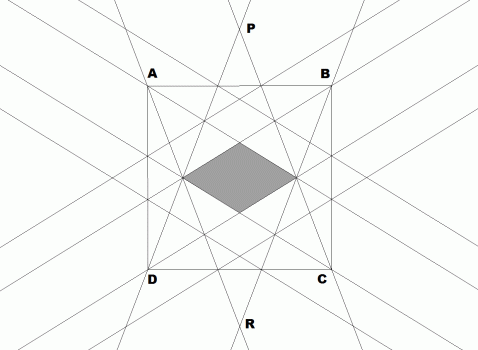
rys. 5

Poprowadźmy jeszcze proste PA, PB, RC oraz RD. W ten sposób wokół kwadratu powstał romb PQRS (rys. 6).

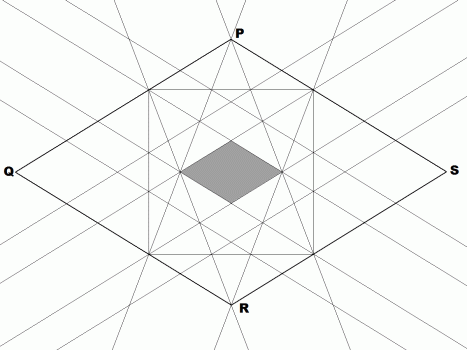
rys. 6

Można wykazać, że stosunek jego przekątnych jest również liczbą złotą. Wielościan wyznaczony przez 30 takich rombów to nasz tytułowy bohater - trzydziestościan rombowy wielki (rys. 7).

rys. 7

Widoczne na zewnątrz fragmenty ścian są na rysunku 8 zacieniowane.

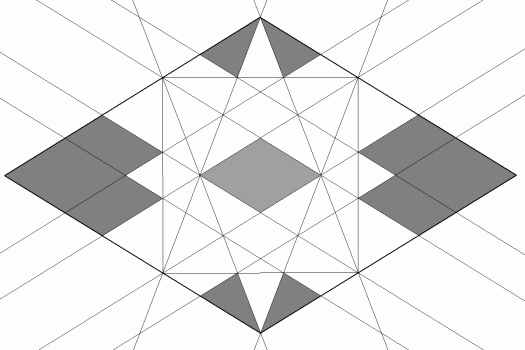
rys. 8

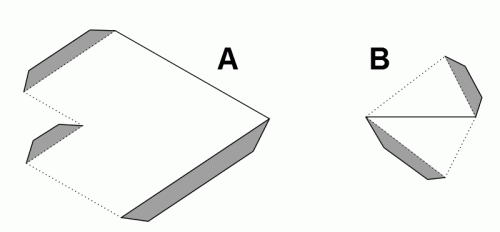
Wykonanie modelu tego wielościanu nie jest specjalnie trudne, choć wymaga wiele staranności. Elementy siatki przedstawia rysunek 9.

rys. 9

Cały model składa się z 12 „kwiatków”. Każdy z nich złożony jest z 5 płatków (część A) i „dna”, które powstaje w wyniku sklejenia 5 części B. Kliknięcie w rysunek 9 otwiera w nowym oknie zestaw elementów potrzebnych do wykonania dwóch „kwiatków”. Linie przerywane oznaczają krawędzie wklęsłe. Po przygotowaniu „kwiatków” łączymy je w całość. W opisany wyżej sposób powstanie model jednobarwny. Aby uzyskać model kolorowy, można albo pomalować ściany, używając 5 kolorów, albo spróbować większego wyzwania i, wycinając każdy element oddzielnie, wykonać model z 5 kolorów kartonu (jak na zdjęciu poniżej).

Na koniec zwróćmy uwagę na jeszcze jeden fakt. Opisany wielościan ma 32 wierzchołki. Można zauważyć, że 20 z nich wyznacza foremny dwunastościan, a pozostałe 12 to wierzchołki dwudziestościanu foremnego (rys. 10).

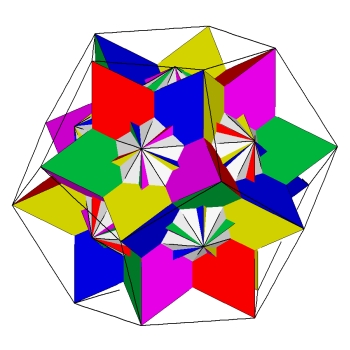
rys. 10

Co więcej, odpowiednie krawędzie tych brył są wzajemnie prostopadłe i (jak można wykazać) wszystkie mają równą długość.

Rysunki i diagramy zostały przygotowane za pomocą programu Wingeom.